Закон электромагнитной индукции

История развития и опыты Фарадея

До середины XIX века считалось, что электрическое и магнитное поле не имеют никакой связи, и природа их существования различна. Но М. Фарадей был уверен в единой природе этих полей и их свойств. Явление электромагнитной индукции, обнаруженное им, впоследствии стало фундаментом для устройства генераторов всех электростанций. Благодаря этому открытию знания человечества о электромагнетизме шагнули далеко вперед.

Фарадей проделал следующий опыт: он замыкал цепь в катушке I и вокруг нее возрастало магнитное поле. Далее линии индукции данного магнитного поля пересекали катушку II, в которой возникал индукционный ток.

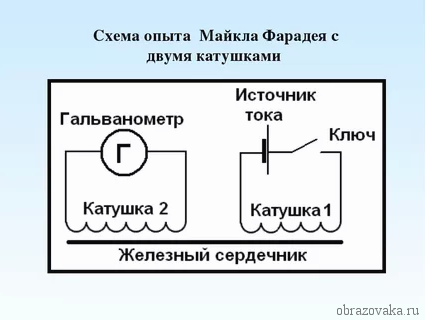
Рис.  Схема опыта Фарадея
На самом деле, одновременно с Фарадеем, но независимо от него, другой ученый Джозеф Генри обнаружил это явление. Однако Фарадей опубликовал свои исследования раньше. Таким образом, автором закона электромагнитной индукции стал Майкл Фарадей.

Сколько бы экспериментов не проводил Фарадей, неизменным оставалось одно условие: для образования индукционного тока важным является изменение магнитного потока, пронизывающего замкнутый проводящий контур (катушку).

Основные понятия

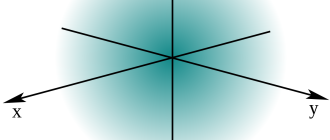
Формулировка закона электромагнитной индукции становится более понятной после изучения тех характеристик, которые в нем упоминаются. Определение свойств магнитного поля основывается на знании вектора напряжённости в каждой его точке. Зрительно это можно представить в виде картинки с большим количеством стрелок. Если поле является неравномерным, то они могут иметь различные направления и величину. Магнитное поле способно с течением времени изменяться. В этом случае напряжённость будет принимать различные значения.

Закон электромагнитной индукции Фарадея рассматривает замкнутый контур. Подразумевается, что он сделан из проводника и имеет произвольную форму. Действие закона относится как к плоским, так и к объёмным замкнутым контурам. Однако для лучшего понимания следует представить себе фигуру простой формы, находящуюся в одной плоскости.

На приведённой здесь схеме показана напряжённость поля B, имеющая вектор, проходящий через плоскость, ограниченную контуром в виде прямоугольника. Перпендикулярное направление к ней обозначено символом n.

Если поле имеет сложную конфигурацию, а также изменяется во времени, то рассматриваются промежутки, которые настолько малы, что вектор в их пределах почти не изменяется. В данном случае напряжённость электрического поля будет представлять собой сумму таких векторов.

Аналогичный подход применяется при рассмотрении сложных поверхностей, ограниченных контуром. Для проведения анализа они разбиваются на элементарные плоские участки. Вычисления в таких сложных случаях производятся с использованием методов интегрального исчисления.

Далее рассматривается контур в виде плоской фигуры с проходящим через него постоянным вектором напряжённости.

Теперь определим, что представляет собой магнитный поток. Расчёты проводятся для определённого поля, проходящего через рассматриваемый контур. Используется следующая формула:

Из формулы видно, что если рамка перпендикулярна вектору напряжённости, то магнитный поток будет максимальным, а если параллельна, то он равен нулю. Поток может принимать положительное или отрицательное значение в зависимости от величины косинуса угла.

Опыты Фарадея. Электромагнитная индукция

Опыты Фарадея известны из школьного курса, наглядно представленные на рисунке.

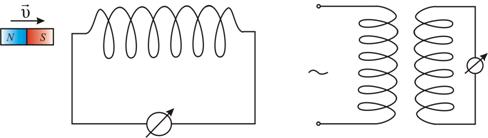
Рисунок . Возникновение электрического тока при поднесении или вытягивании катушки с левой стороны и возникновение электрического тока с двумя близко расположенными катушками справа.

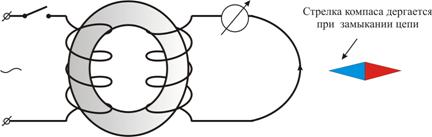
Рисунок . Возникновение электрического тока при соединении катушек сердечником.

Определение 1

На данный момент опыты Фарадея называют классическими и применяют для обнаружения электромагнитной индукции:

1. Замыкание гальванометра на соленоиде. В соленоид опускается постоянный магнит, перемещая который, фиксируются отклонения стрелки гальванометра. Это говорит о наличии индукционного тока. Если увеличить скорость перемещения магнита относительно катушки, тогда стрелка гальванометра отклонится еще сильнее. Это говорит о том, что произошла замена полей. Магнит может быть неподвижным или передвижение соленоида происходит относительно магнита.
2. Две катушки. Производится установка одной в другую. Концы одной из них подключаются с гальванометром. Другая катушка подвергается прохождению тока. При его подаче и отключении стрелка гальванометра изменяет свое положение. В этом случае катушки должны находиться в движении относительно друг друга. Стрелка гальванометра уменьшает значение при его включении.

Определение 2

При изменении потока вектора индукции, пронизывающего проводящий контур, происходит возникновение электрического тока, что называется явлением электромагнитной индукции, а такой ток – индукционным.

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Опыты Фарадея

• На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
• Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
• Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• источник – переменное магнитное поле;
• обнаруживается по действию на заряд;
• не является потенциальным;
• линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

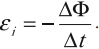
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​( N )​ витков, то ЭДС индукции:

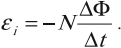
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​( R )​:

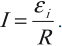
При движении проводника длиной ​( l )​ со скоростью ​( v )​ в постоянном однородном магнитном поле с индукцией ​( vec{B} )​ ЭДС электромагнитной индукции равна:

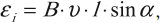
где ​( alpha )​ – угол между векторами ​( vec{B} )​ и ( vec{v} ).

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
• вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

• определить направление линий магнитной индукции внешнего магнитного поля;
• выяснить, как изменяется магнитный поток;
• определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
• по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Магнитный поток

Понятие магнитного потока как раз и является характеристикой количества линий магнитного поля, пронизывающих контур.

Для простоты мы ограничиваемся случаем однородного магнитного поля. Рассмотрим контур площади
, находящийся в магнитном поле с индукцией
.

Пусть сначала магнитное поле перпендикулярно плоскости контура (рис. 1).

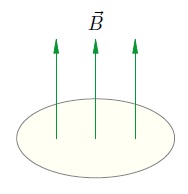
Рис. 1.

В этом случае магнитный поток
определяется очень просто — как произведение индукции магнитного поля на площадь контура:

(1)

Теперь рассмотрим общий случай, когда вектор
образует угол
с нормалью к плоскости контура (рис. 2).

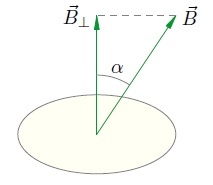
Рис. 2.

Мы видим, что теперь сквозь контур «протекает» лишь перпендикулярная составляющая
вектора магнитной индукции
(а та составляющая, которая параллельна контуру, не «течёт» сквозь него). Поэтому, согласно формуле (1), имеем
. Но
, поэтому

(2)

Это и есть общее определение магнитного потока в случае однородного магнитного поля. Обратите внимание, что если вектор
параллелен плоскости контура (то есть
), то магнитный поток становится равным нулю.

А как определить магнитный поток, если поле не является однородным? Укажем лишь идею. Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2), а затем все эти магнитные потоки суммируем.

Единицей измерения магнитного потока является вебер (Вб). Как видим,

Вб = Тл · м
= В · с. (3)

Почему же магнитный поток характеризует «количество линий» магнитного поля, пронизывающих контур? Очень просто. «Количество линий» определяется их густотой (а значит, величиной
— ведь чем больше индукция, тем гуще линии) и «эффективной» площадью, пронизываемой полем (а это есть не что иное, как
). Но множители
и
как раз и образуют магнитный поток!

Теперь мы можем дать более чёткое определение явления электромагнитной индукции, открытого Фарадеем.

Электромагнитная индукция — это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур.

ЭДС индукции

Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы — сторонние силы, вызывающие движение зарядов.

Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС):
. В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции и обозначается
.

Итак, ЭДС индукции
— это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура.

Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.

В чем заключается явление электромагнитной индукции?

В общем смысле явление электромагнитное индукции заключается в генерации электрического тока с помощью магнитного поля.

Скажем точнее, явление электромагнитной индукции заключается в образовании электродвижущей силы (ЭДС) в проводнике в результате изменения потока магнитного поля, пронизывающего поверхность, охватывающую проводник. В замкнутой цепи электродвижущая сила (ЭДС) вызывает протекание электрического тока.

В приведенном выше определении явления могут быть неясными два понятия – ЭДС индукции и магнитный поток.

ЭДС индукции.

Абсолютная величина электродвижущей силы ( ЭДС индукции с символом εинд ) есть работа внешней силы Az, которая вызывает перемещение единичного заряда по цепи. Следовательно: | εинд | = Az / q .

Как видите, в определении мы использовали абсолютное значение ЭДС индукции. Это потому, что оно может быть отрицательным, при определенных ситуациях. С другой стороны, работа внешних сил, согласно принципу сохранения энергии, всегда, при генерации электрического тока, должна быть положительной.

Определение потока магнитной индукции.

Поток магнитной индукции B через поверхность S называется скалярным произведением векторов B и S: dФ = B * S * cos α , где α – угол между двумя векторами, а S – вектор, перпендикулярный поверхности S с величиной, равной площади этой поверхности.

Магнитный поток будет меняться при изменении любой величины, входящей в формулу – площади поверхности, значения магнитной индукции, угла между площадью поверхности и вектором индукции – при сохранении постоянства остальных переменных. Конечно, все эти величины могут изменяться одновременно, но таким образом, что их произведение не остается постоянным.

О том, что электрический ток является источником магнитного поля, было известно с 1820 года (работа Орстеда). Фарадей задался вопросом, не верно ли и обратное – не может ли магнитное поле быть источником (причиной) электрического тока. Однако дело оказалось не таким простым. Только в 1831 году ученый наблюдал это явление при определенных особых обстоятельствах. Оказалось, что при стабильных условиях электрический ток не возникает.

Почему это происходит? Даже в очень сильном, но постоянном во времени магнитном поле электрический ток не будет течь в замкнутой цепи “сам по себе”. Он течет только тогда, когда мы соответствующим образом перемещаем контур или изменяем магнитное поле, в котором находится контур.

Когда Фарадей обратил внимание на условия, при которых в присутствии магнитного поля возникает электрический ток, он провел десятки экспериментов, которые обобщил и из которых сделал количественные выводы в виде закона электромагнитной индукции. Мы не будем здесь говорить об этом законе, а сосредоточимся только на сути явления электромагнитной индукции. Мы попытаемся увидеть двойственность этого явления, т.е. то, что оно имеет две разновидности, и ответить на вопрос, почему электрический ток течет при определенных условиях.

Мы рассмотрим, какие силы вызывают индукционный ток, т.е. какие силы действуют на свободные заряды в проводнике, заставляя их двигаться.

Эксперимент Фарадея 1831 года, демонстрирующий электромагнитную индукцию между двумя катушками (см. рисунок ).

Справа находится аккумулятор, питающий меньшую из двух катушек (A), которая создает магнитное поле. Когда эта катушка находится в состоянии покоя, индукционный ток не наблюдается. Однако если переместить его внутрь большей катушки (B), переменный магнитный поток индуцирует в ней ток. Мы обнаруживаем это, наблюдая за колебаниями стрелки гальванометра (G) слева.

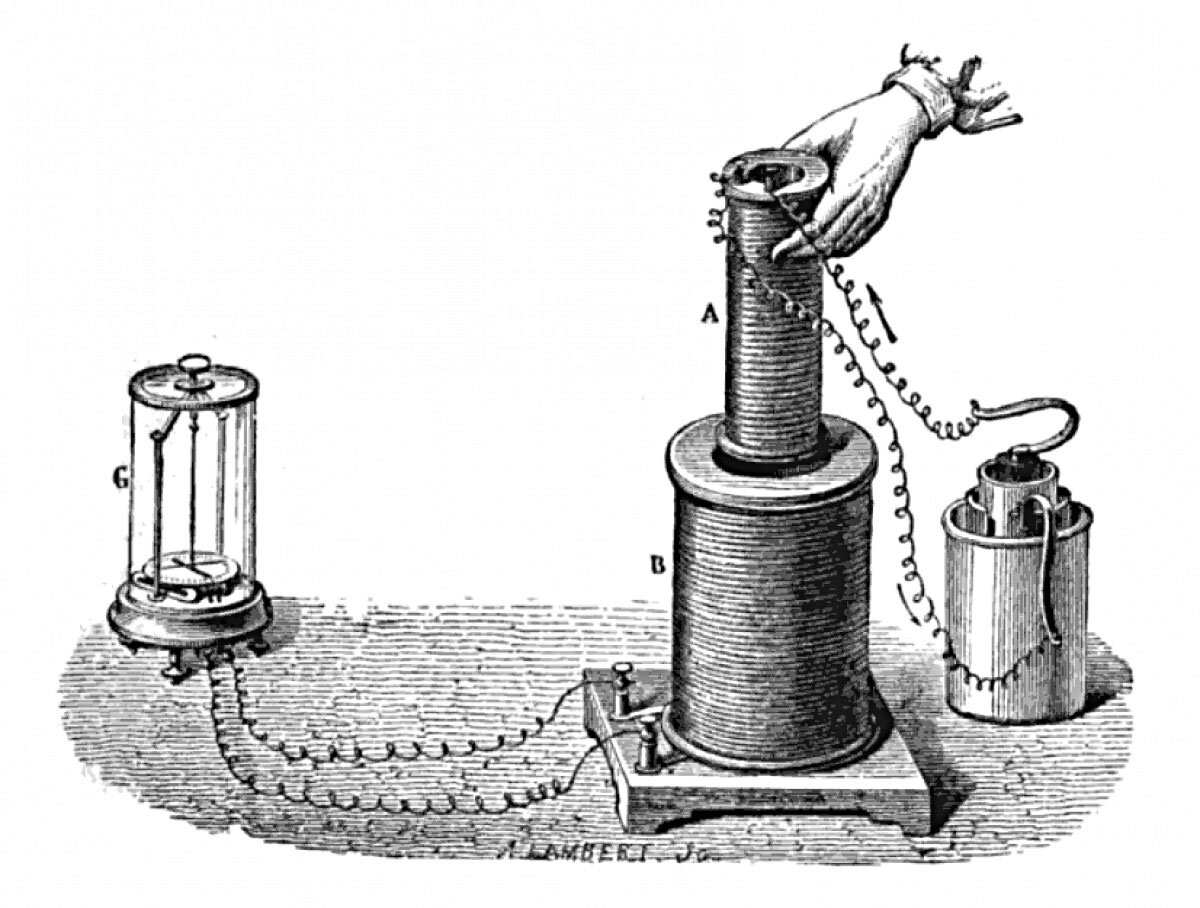
Рис. 1. Эксперимент Фарадея 1831 года, демонстрирующий электромагнитную индукцию между двумя катушками (см. рисунок ).

Закон Фарадея в дифференциальной форме

Чтобы сформулировать закон Фарадея в такой форме, нам потребуется вспомнить несколько базовых формул.

1. ЭДС индукции: εi=-υBl.
2. Магнитный поток: Φ=∫SBndS.
3. Теорема Стокса: ∮l=a→dl=∫Srotna→dS.

Используя данные выражения, мы можем записать следующую формулу:

∮C(Edl)=∫S(n rot E)dS=-1c∫Sn∂B∂tdS.

Здесь S обозначает поверхность, натянутую на контур S. Поскольку значение S является произвольным, то мы можем записать:

Определение 4

rot E=-1c∂B∂t.

Это и есть дифференциальная форма закона Фарадея, которая описывает возникновение электрического поля в точке при изменении магнитного поля в том же месте. Само поле при этом называется индукционным.

Определение 5

Индукционное поле не является потенциальным, в отличие от электростатического, а работа по перемещению заряда в нем по замкнутому контуру не является нулевой.

Объединённый закон

Для определения количественных показателей электрохимических реакций на практике используется объединённый закон Фарадея.

Обобщенный закон можно представить в виде такой формулировки: отношение массы полученного вещества к его химическому эквиваленту равно отношению использованного заряда к тому, который надо потратить на извлечение одного моля вещества.

Задачи на применение закона Фарадея

Пример 1

Условие: проволочный контур помещен в магнитное поле. В нулевой момент времени он пронизывает поток магнитной индукции, равный Φ1 и уменьшающийся после этого до 0. Найдите величину заряда, проходящего по цепи.

Решение

Начнем с определения мгновенного значения ЭДС. Это можно сделать с помощью формулы:

εi=-dΦdt.

Вспомним закон Ома. Согласно ему, мгновенное значение силы тока может быть записано в следующем виде:

I=-1RdΦdt.

Полное сопротивление цепи здесь обозначено буквой R.

Для нахождения заряда, идущего по цепи, нам пригодится выражение:

q=∫Idt.

Поставим эти выражения в нужную формулу и получим:

q=-1R∫Φ10dΦ=ΦR.

Автором этой формулы является Фарадей. Он эмпирически подтвердил прямую пропорциональность величины заряда, идущего по цепи, количеству линий магнитной индукции, пересекающей проводник, и его обратную пропорциональность величине сопротивления в цепи.

Ответ: q=ΦR.

Пример 2

Условие: квадратная рамка со стороной a помещена в одну плоскость с проводником, сила тока которого равна l. Она движется поступательно с постоянной скоростью v в направлении, обозначенное на иллюстрации ниже. Вычислите ЭДС индукции как функцию εi от расстояния x.

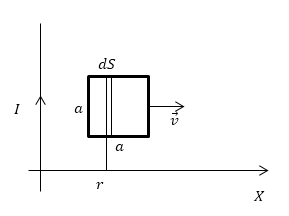
Рисунок 1

Решение

Найти ответ можно с помощью закона Фарадея.

εi=-dΦdt.

Для получения искомой функции Ei(x) нам нужно построить функцию Ф(x). Бесконечный проводник с током создает магнитное поле, которое может быть выражено так:

B=μ0I2πr.

Расстояние до точки рассмотрения здесь обозначено буквой r.

Для решения нам нужно также выделить площадь рамки. Выразим ее такой формулой:

dS=adr.

С учетом приведенных выше выражений, а также того факта, что B→⊥S→, мы можем найти величину элементарного магнитного потока, проходящего через элемент квадратной рамки, так:

dΦ=BdS=μ0I2πradr.

Далее вычисляем величину полного потока, учитывая, что x≤r≤x+a:

Φ=∫xx+aμ0I2πradr=μ0Ia2πlnx+ax.

После этого переходим к нахождению ЭДС индукции с помощью закона Фарадея и выражения для магнитного потока, выведенного ранее:

εi=-dΦdx·dxdt=-μ0Ia2π·xx+a(x-1-(x+a)x-2)·υ==-μ0Ia2π·xx+ax-x-ax2=μ0Ia2υ2π(x+a)x.

Ответ:εi=μ0Ia2υ2π(x+a)x.

Причины возникновения индукционного тока в движущихся и неподвижных проводниках

Причин, по которым может происходить изменение магнитного потока, пронизывающего замкнутый контур, две:

1. Изменение магнитного потока вследствие перемещения всего контура или отдельных его частей в магнитном поле, которое не изменяется со временем;
2. Изменение магнитного поля при неподвижном контуре.

Перейдем к рассмотрению этих случаев подробнее.

Перемещение контура или его частей в неизменном магнитном поле

При движении проводников и свободных носителей заряда в магнитном поле возникает ЭДС индукции. Объяснить возникновение δинд можно действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца здесь – это сторонняя сила.

Пример 2

На рисунке мы изобразили пример индукции, когда прямоугольный контур помещен в однородное магнитное поле B→ направленное перпендикулярно плоскости контура. Одна из сторон контура перемещается по двум другим сторонам с некоторой скоростью.

Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Отражена составляющая силы Лоренца, которая действует на свободный электрон

На свободные заряды подвижной части контура воздействует сила Лоренца. Основная составляющая силы Лоренца в данном случае направлена вдоль проводника и связана с переносной скоростью зарядов υ→. Модуль этой сторонней силы равен:

FЛ=eυ→B.

Работа силы FЛ на пути l равна:

A=FЛ·l=eυBl.

По определению ЭДС:

δинд=Ae=υBl.

Значение сторонней силы для неподвижных частей контура равно нулю. Для соотношения δинд можно записать другой вариант формулы. Площадь контура с течением времени изменяется на ΔS=lυΔt. Соответственно, магнитный поток тоже будет с течением времени изменяться: ΔΦ=BlυΔt.

Следовательно,

δинд=∆Φ∆t.

Знаки в формуле, которая связывает δинд и ∆Φ∆t, можно установить в зависимости от того, какие направления нормали и направления контура будут выбраны. В случае выбора согласованных между собой по правилу правого буравчика направлений нормали n→ и положительного направления обхода контура l→ можно прийти к формуле Фарадея.

При условии, что сопротивление всей цепи – это R, то по ней будет протекать индукционный ток, который равен Iинд=δиндR. За время Δt на сопротивлении R выделится джоулево тепло:

∆Q=RIинд2∆t=υ2B2l2R∆t

Парадокса здесь нет. Мы просто не учли воздействие на систему еще одной силы. Объяснение заключается в том, что при протекании индукционного тока по проводнику, расположенному в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, которая связана с относительной скоростью движения зарядов вдоль проводника. Благодаря этой составляющей появляется сила Ампера FА→.

Для рассмотренного выше примера модуль силы Ампера равен FA =IBl. Направление силы Ампера таково, что она совершает отрицательную механическую работу Aмех. Вычислить эту механическую работу за определенный период времени можно по формуле:

Aмех=-Fυ∆t=-IBlυ∆t=-υ2B2l2R∆t

Проводник, перемещающийся в магнитном поле, испытывает магнитное торможение. Это приводит к тому, что полная работа силы Лоренца равна нулю. Джоулево тепло может выделяться либо за счет уменьшения кинетической энергии движущегося проводника, либо за счет энергии, которая поддерживает скорость перемещения проводника в пространстве.

Изменение магнитного поля при неподвижном контуре

Определение 3

Вихревое электрическое поле – это электрическое поле, которое вызывается изменяющимся магнитным полем.

В отличие от потенциального электрического поля работа вихревого электрического поля при перемещении единичного положительного заряда по замкнутому проводящему контуру равна δинд в неподвижном проводнике.

В неподвижном проводнике электроны могут приводиться в движение только под действием электрического поля. А возникновение δинд нельзя объяснить действием силы Лоренца.

Первым, кто ввел понятие вихревого электрического поля, был английский физик Джон Максвелл. Случилось это в 1861 году.

Фактически, явления индукции в подвижных и неподвижных проводниках протекают одинаково. Так что в этом случае мы тоже можем использовать формулу Фарадея. Отличия касаются физической причины возникновения индукционного тока: в движущихся проводниках δинд обусловлена силой Лоренца, в неподвижных – действием на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

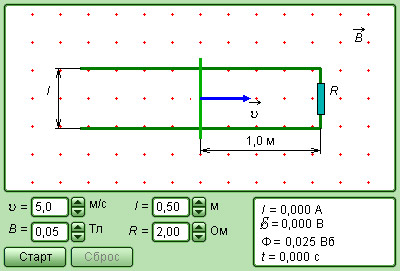
Рисунок  Модель электромагнитной индукции

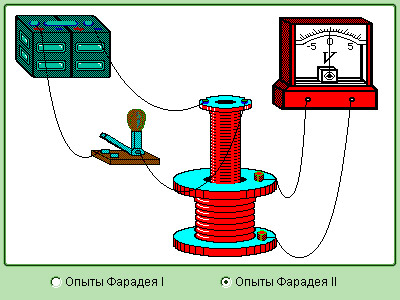
Рисунок  Модель опытов Фарадея

Практическое применение закона Фарадея

Эффект, который описывается рассматриваемым законом, позволяет превращать механическое движение в электрический ток. Это можно объяснить с помощью следующего примера.

Если постоянный магнит перемещать вдоль замкнутого контура, то по нему пройдёт ток. Его сила будет зависеть от особенностей движения магнита. Понятно, что механическое движение можно обеспечить множеством различных способов. Однако в результате применения указанной схемы можно получить электрическую энергию.

Закон Фарадея также используется в работе трансформаторов. Они устроены таким образом, что переменный ток подаётся на входную катушку (первичную обмотку). Его изменения создают магнитное поле в сердечнике, которое также проходит через вторую катушку (вторичную обмотку). Изменения магнитного поля создают ток, используемый для работы электроприбора.

Токовые клещи представляют собой особый тип трансформатора. Обычно сердечник имеет форму кольца, но в токовых клещах он разомкнут. Этот инструмент можно раскрыть и затем закрыть вокруг провода, бесконтактным образом измеряя силу тока в нём. Такие измерения проводятся без отключения электросети, что существенно упрощает процедуру.

Закон Фарадея в относительно простой и понятной форме описывает связь между электрическим и магнитным полями. Он является основным законом электродинамики. На его основе построен принцип работы генераторов и электродвигателей.