Введение

Рис. Зависимости холловского сопротивления и удельного сопротивления от магнитного поля при постоянной концентрации носителей. На зависимости холловского сопротивления наблюдаются «плато» [4] .
Эффект состоит в том, что при достаточно низких температурах в сильных магнитных полях на графике зависимости поперечного сопротивления (отношения возникающего поперечного напряжения к протекающему продольному току) вырожденного двумерного электронного газа (ДЭГ) от величины нормальной составляющей к поверхности ДЭГ индукции магнитного поля (или от концентрации при фиксированном магнитном поле) наблюдаются участки с неизменным поперечным сопротивлением или «плато».
Фон Клитцинг обнаружил так называемый нормальный (или целочисленный) квантовый эффект Холла (КЭХ), когда значения сопротивления на «плато» равно ρxy=h/νe2{displaystyle rho _{xy}=h/nu e^{2}}
, где e — заряд электрона, h — постоянная Планка, ν — натуральное число, называемое фактором заполнения уровней Ландау (рис.).
В 1982 году Д. Цуи и Х. Штёрмер открыли дробный квантовый эффект Холла (фактор заполнения при этом становится меньше единицы).
Уже первая работа по КЭХ, названная «Новый метод определения постоянной тонкой структуры с высокой точностью по квантованию холловского сопротивления» показала, что возможно его применение в качестве стандарта сопротивления. В настоящее время известно, что значения квантованного сопротивления Холла не зависят от качества образца и его материала. Поэтому, начиная с 1990 года, калибровки сопротивлений основаны на КЭХ с фиксированным значением Rэ = 25812.807557(18) Ом.
Для наблюдения КЭХ существует ряд условий, которые должны выполняться, чтобы квантование было точным. Ниже приведены основные предпосылки возникновения плато.
Что такое квантовый эффект Холла — описание явления
Определение
Эффект Холла — это явление возникновения поперечной разности потенциалов при помещении проводника с постоянным током в магнитное поле.
Данный эффект был открыт в 1879 году Эдвином Холлом в тонких пластинках золота, когда ученый обнаружил на их краях разность потенциалов.
Принцип измерения: при помещении в магнитное поле пластины-проводника под 90 градусов к направлению силовых линий магнитного потока, произойдет перемещение электронов по поперечине пластины под действием силы Лоренца — силы, с которой электромагнитное поле действует на точечную заряженную частицу.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: avatars.mds.yandex.net
Таким образом, эффект Холла выражается действием магнитного поля на заряженную частицу.
Пример эффекта в жизни
Если взять обычный провод, по которому течет электрический ток, и использовать магнитное поле, можно создать новое электрическое напряжение. Оно будет перпендикулярно потоку тока. Этот и есть так называемый эффект Холла.

Квантовое туннелирование в фазовом пространстве.
Существует его соответствующая квантовая версия эффекта, который возникает с определенными приращениями, или квантами. Это открыло возможность использования квантового аномального эффекта Холла для создания новых высокопроводящих проводов или даже квантовых компьютеров. Однако физика, которая приводит к этому явлению, до сих пор полностью не изучена.
В чем заключается квантовый эффект Холла
Определение 1
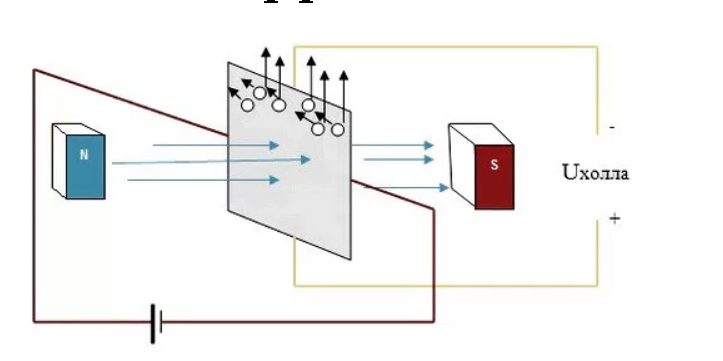
При помещении в магнитное поле пластины-проводника или полупроводника под 90 °к направлению силовых линий магнитного потока произойдет перемещение электронов по поперечине пластины под действием силы Лоренца. Их направление зависит от того, в какую сторону идет сила тока и силовые линии магнитного потока. Иначе говоря, (ЭХ) эффект Холла – это частный случай действия силы Лоренца, то есть действия магнитного поля на заряженную частицу.
Это можно рассмотреть на простейшем примере.
Пример 1
Если представить расположенную к нам торцом пластину, то ее кромка направлена вниз. Она сделана из металла, оба торца подключены к источнику питания, задний из которых на минус, передний на плюс.
Данный случай говорит о том, что электрический ток будет протекать по направлению к наблюдателю. Справа и слева от пластины располагаются два магнита. Правый из них обращен к пластине северным полюсом, левый – южным. Делаем вывод, что данный случай показывает направление силовых линий магнитного поля справа налево, так как они всегда выходят из северного полюса и входят в южный. Силовые линии отклоняют электроны, которые проходят по пластине к ее верхней кромке.
При изменении направления тока в пластине при помощи перемены местами проводников мы сможем наблюдать отклонение электронов вниз. Если направление не менять, а только лишь полюса магнитов, электроны начнут сдвигаться вниз. Когда применяются оба направления, сила Лоренца произведет их перемещение вверх.
Очевидно, что одна из кромок накапливает отрицательный заряд под действием силы Лоренца, на другая на противоположной стороне – положительный. Это говорит о наличии разности потенциалов между ними, то есть электрического напряжения. Увеличение этой разности будет происходить до тех пор, пока не уравновесит силу Лоренца.
Определение 2
Возникновение разности потенциалов в таких случаях, получило название напряжения Холла, которое можно рассчитать, используя формулу:
Uхолл=-IBet, где I является силой тока, B – вектором магнитной индукции, e – зарядом электрона, p – количеством электронов в единице объема, t – толщиной пластины.
В чем суть, как объяснить простыми словами
Описание механизма работы: к проводящему проводнику подводится электрический ток, затем гальванометр подключается к его краям. Далее электромагнит включается так, чтобы линии напряженности поля лежали перпендикулярно плоскости пластины.
Таким образом предполагалось выявить условия для изменения протекания тока. В результате было обнаружено, что при подаче на тонкий лист золота электрического тока заряд в ней распределялся равномерно по всей поверхности. Но как только добавляется ток — заряд переходит к краям и возникает разность потенциалов.
Именно на этом открытии позже были построены одноименные датчики.
Физическое объяснение эффекта Холла
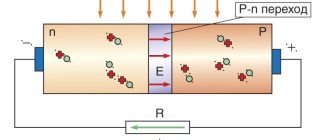
Если приложить напряжение к электрическому проводнику, называемому здесь образцом, потечет электрический ток. Электроны движутся по проводнику со средней скоростью v, также называемой скоростью дрейфа. Если держать образец в стационарном магнитном поле, то на электроны действует сила Лоренца. Это вызывает отклонение электронов перпендикулярно движению. Это вызывает избыток электронов на стороне отклонения и соответствующий недостаток электронов на противоположной стороне.
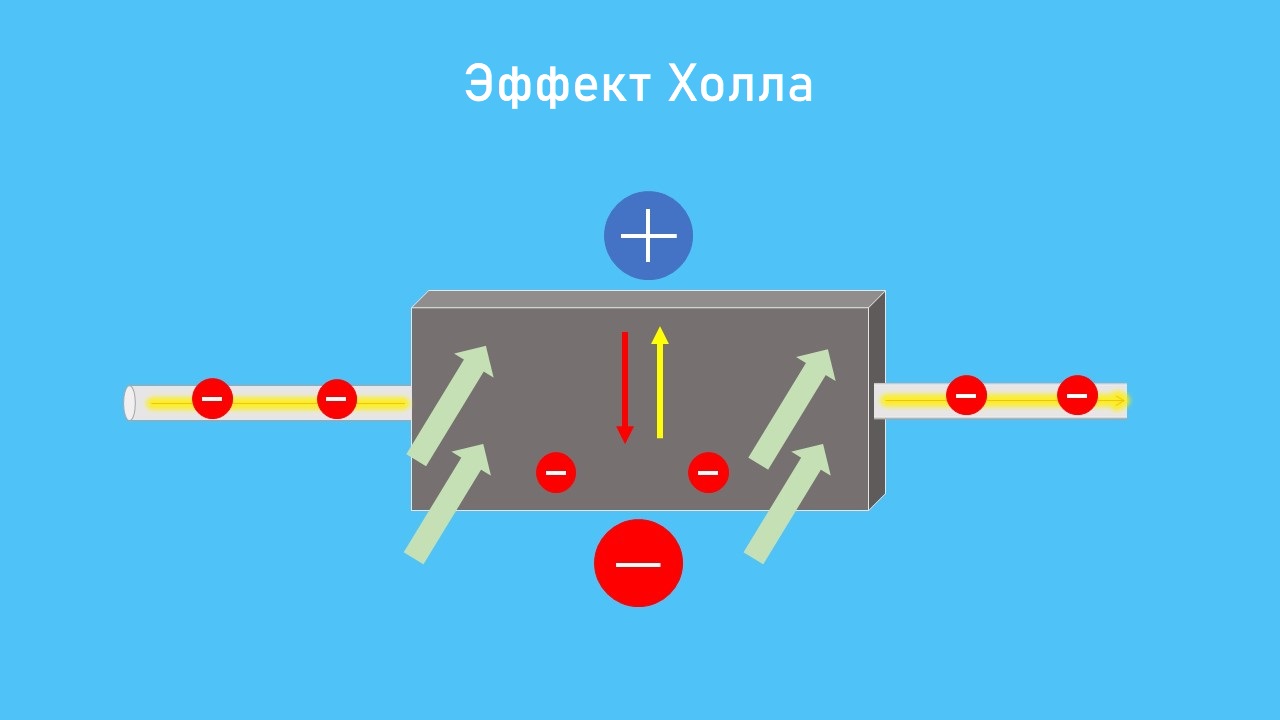
Рис. Эффект Холла: избыток и недостаток электронов
Вы можете представить себе это разделение зарядов как сходное с разделением зарядов в конденсаторе. Поскольку положительно и отрицательно заряженные стороны теперь находятся напротив друг друга, создается электрическое поле. Это электрическое поле оказывает на электроны силу, противоположную силе Лоренца. Если эти две силы компенсируют друг друга в одинаковой степени, то усиление разделения зарядов заканчивается.
Как и в случае с конденсатором, здесь можно отводить напряжение. Это электрическое напряжение называется напряжением Холла. Это напряжение Холла линейно возрастает с увеличением магнитного поля и антипропорционально плотности носителей заряда. Это объясняется тем, что неизменная сила тока при меньшем числе носителей заряда может быть достигнута только за счет большей скорости отдельных носителей заряда. Более сильная сила Лоренца действует на более быстрые носители заряда, что увеличивает напряжение Холла.
Вычисление напряжения Холла
Для того чтобы понять вывод напряжения Холла, необходимо базовое понимание векторного исчисления.
Здесь вы можете увидеть набросок расчета напряжения Холла. Он действителен только для одного типа носителей заряда, например, для металлических образцов.
Сила Лоренца, действующая на проводник в магнитном поле, задается следующим образом:
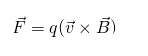
Где, сила Лоренца F, q – электрический заряд, v – скорость и магнитное поле B. В эффекте Холла возникает электрическое поле E, которое нейтрализует отклоняющую силу магнитного поля. Поэтому:
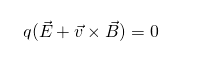
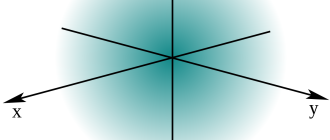
Для упрощения зададим систему координат так, чтобы носители заряда двигались в направлении x, а магнитное поле действовало в направлении z. Это дает v = ( vx, 0, 0 ) и B = ( 0, 0, Bz ). После деления на q получается y-компонента:
Ey – vxBz = 0
Плотность тока J в проводнике выражается через J = n*q*v, при плотности носителей заряда n. Если преобразовать это уравнение в vx и подставить его в вышеприведенное уравнение, то получится:
Ey = jx * Bz * ( 1 / n * q ) = AH * jx * Bz.
Мы определили коэффициента Холла AH, которая характеризует силу эффекта Холла.
Поскольку вы уже знаете, что можно рассматривать разделение зарядов аналогично разделению в конденсаторе, то для упрощения можно использовать следующее обозначение:
Ey = UH / b
Плотность тока в этом случае может быть выражена через jx = I / b*d, где I – сила тока, b – ширина проводника и d – толщина проводника. Подставляя оба выражения, получаем для напряжения Холла следующее выражение:
UH = AH * ( I * Bz / d )
Расчёт коэффициента Холла
В качестве примера представьте медную пластину (ширина b = 18 мм, толщина d = 0,001 м). Она вносится в магнитное поле с плотностью магнитного потока B = 1,2 Тл. Если через пластину протекает электрический ток I = 15 А, то можно измерить напряжение Холла UH = – 1,02 * 10-6 В .
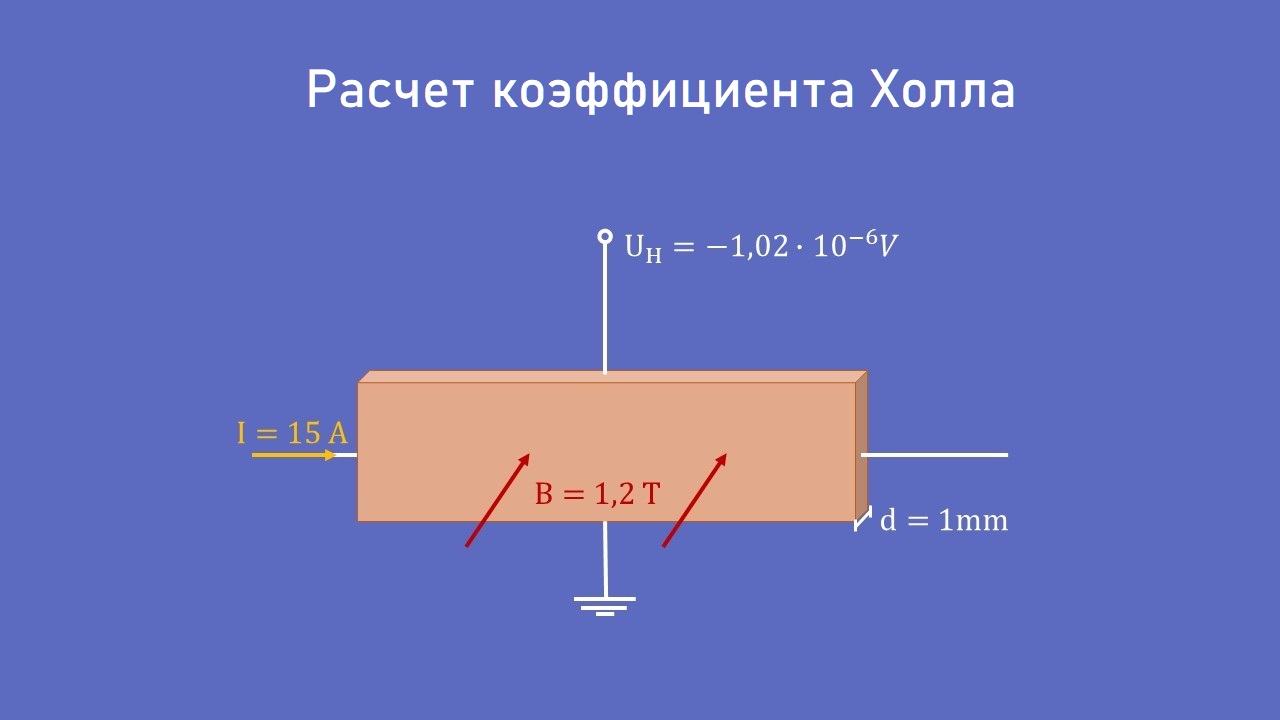
Рис. Расчет коэффициента холла
Если взять приведенную выше формулу и преобразовать ее в AH, то получится: AH = UH * d / I * B .
Подставляя значения, можно вычислить коэффициент Холла, то есть: AH = – 1,02 * 10-6 * 0,001 / 15 * 1,2 = – 5,7 * 10-11 мм3 / Кл
По их отрицательному знаку видно, что это электроны, а не дырки или положительные заряды.
Обозрение процессов
Рассмотрим эффект Холла с точки зрения протекания процессов в определенном проводнике на простейшем примере. Допустим, имеется брусок, который проводит электрический ток и при этом находится в м. п. со слабым потенциалом и под векторным напряжением электрического поля E. Находясь в таких условиях, носитель заряда (н. з.) будет отклоняться от м. п. в сторону одной из граней бруска либо противоположно по отношению к электрическому полю, либо вдоль от движения самого носителя. Показатель критерия малости в данном случае будет служить необходимостью, при которой н. з. не начинает движение по трансцендентной кривой плоскости.
В результате данного протекания процесса, сила Лоренца создаст условия, вызывающие накопление зарядов с отрицательным показателем, около одной грани бруска, а в противовес на другой грани будет накапливаться положительный заряд. Будет происходить накопление заряда до тех пор, пока образовавшееся поле не сможет компенсировать магнитный компонент составной силы Лоренца. Величина электронной скорости выражается при помощи плотности тока. RH, который в данном случае равен и пропорционален E1 и jB. Подобное явление называют константой Холла, или его коэффициентом.
Такое приближение носит знак постоянной Холла и зависит от н. з. Это дает возможность определять их тип для большого количества металлов. Например, определенные металлы в поле с высокими показателями силы носят положительный знак RH, а объяснение этому дают квантовая и полуклассическая теория твердых тел.
Аномальный эффект Холла
Случай появления напряжения (электрического поля) в образце, перпендикулярного направлению пропускаемого через образец тока, наблюдающегося в отсутствие приложенного постоянного магнитного поля (то есть явление, полностью аналогичное эффекту Холла, но наблюдающееся без внешнего постоянного магнитного поля), называется аномальным эффектом Холла.
Необходимым условием для наблюдения аномального эффекта Холла является нарушение инвариантности по отношению к обращению времени в системе. Например, аномальный эффект Холла может наблюдаться в образцах с намагниченностью.
Способы использования явления
На основе эффекта Холла создаются устройства и приборы, обладающие нужными и часто уникальными свойствами
Эти приборы занимают важное место в измерительно-контрольной технике, автоматизации, радиотехнике и т. д
Приспособления, использующие в своей работе явление Холла, называются элементами Холла (датчиками).
Эти датчики дают возможность измерять силу магнитного поля, так как при неизменной величине тока электродвижущая сила прямо пропорциональна линиям магнитной индукции. Прямая зависимость этих величин для элементов Холла является неоспоримым преимуществом перед другими типами измерителей индукции, основанных на контроле магнетосопротивления.
Приборы Холла позволяют проводить измерения электрических и магнитных характеристик не только металлов, но и полупроводников. Из-за простоты своего действия, несложности в изготовлении, а также высокой точности и надёжности они широко применяются в различных отраслях науки и техники. Датчики используются для измерения силы, давления, углов, перемещения и других неэлектрических величин. Этот эффект используют и при изготовлении полупроводников для контроля подвижности носителей зарядов и подсчёта их концентрации.
Для этого используется формула эффекта Холла: V h = j*B*H / n*q = B*I / (q*n*α) = R*B*I/α,
из которой число носителей находится как N = (I*B) / (q*α* V h). Таким образом, можно определить не только количество носителей, но и также их тип (знак).
Элементы Холла применяются в автомобилестроении из-за их невысокой стоимости, точности показаний, надёжности и способности не зависеть от условий окружающей среды. Их используют в конструкции бесконтактных однополярных и биполярных прерывателей. Благодаря их миниатюрному исполнению электронные гаджеты можно автоматически включать или выключать экран при открытии или закрытии чехла с магнитом. Они помогают в GPS-навигации, улучшая геопозирование.
С каждым годом эффект Холла находит всё более новое применение. Свидетельством тому служит появление устройства виртуальной реальности — Google Card Board, в основе работы которого лежит взаимодействие магнита с датчиком Холла.
Предыдущая