Сила Ампера и сила Лоренца – формулы и определение правила правой руки кратко (9 класс)

Содержание:

Силы Лоренца и Ампера

Магнитное поле порождается движущимися электрическими зарядами. И в свою очередь электрические заряды, движущиеся в магнитном поле, испытывают силовое воздействие с его стороны.

Сила, действующая на движущийся заряд, называется силой Лоренца.

Магнитные поля не реагируют на неподвижный электрический заряд, так же как не действует сила Ампера на обесточенный проводник.

Для возникновения силы Лоренца необходимо выполнить три условия:

У частицы должен быть отрицательный или положительный заряд.
Заряженная частица должна находиться в магнитном поле.
Частица должна быть в движении, то есть вектор v ≠ 0.

Если хотя бы одно из условий не выполняется, сила Лоренца не возникает

Размерность силы Лоренца в международной системе СИ – ньютон (Н). Разумеется, модуль силы Лоренца настолько крохотная величина, по сравнению с ньютоном, что её записывают в виде К×10-n Н.

Поскольку электрический ток представляет собой упорядоченное движение электрических зарядов, то в случае, когда он протекает через магнитное поле, силы Лоренца, действующие на отдельные носители, складываются в одну общую силу, которая называется силой Ампера.

Сила Ампера

Модуль силы Ампера определяется с помощью формулы, похожей на формулу силы Лоренца:

Схожесть формул объясняется тем, что сила Ампера является макроскопическим проявлением силы Лоренца. Направление действия этих сил совпадает.

Формулы силы Ампера и силы Лоренца

Поскольку сила Ампера — это результат действия силы Лоренца, то и формулы, описывающие эти силы, близки, единицы измерения одинаковы. Сила Ампера и сила Лоренца пропорциональны величине перпендикулярной составляющей индукции, следовательно, эта часть в обеих формулах будет общей. Кроме того, обе этих силы пропорциональны величине заряда и его скорости движения.

Проявление магнитного поля заключается в появлении силы, действующей на проводник с током. Направление этой силы определяется мнемоническим правилом левой руки: если перпендикулярная составляющая индукции магнитного поля $B_{perp}$ входит в ладонь левой руки, а четыре пальца указывают направление электрического тока, то большой палец будет указывать направление силы Ампера. При этом имеется ввиду однородное магнитное поле. Расчет силы Ампера для неоднородного поля значительно сложнее, требует отдельного доклада и выходит за рамки школьной программы по физике.

Формула силы Ампера будет аналогичной, место заряда займет величина тока I (поскольку ток равен отношению заряда, проходящего по проводнику, ко времени прохождения), место скорости займет длина проводника (поскольку скорость равна отношению длины, которую прошел заряд, ко времени этого прохождения).

Рассмотрим случай, когда заряженная частица находится в движении в двух полях одновременно (в электрическом и магнитном), тогда на заряд подействуют две составляющие:

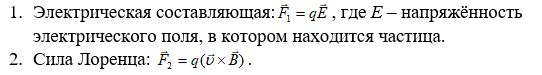
2 составляющие действующие на заряд

Тогда:

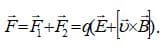
Формула силы Лоренца

Поскольку эту формулу вывел Лоренц, то её также называют именем учёного-физика.

Направление силы Ампера и силы Лоренца

В отличие от многих других сил, направление силы Лоренца (а значит, и силы Ампера) не совпадает с направлением движения носителя и не совпадает с направлением на источник магнитного поля. Для определения направления этих сил используется мнемоническое правило левой руки.

Если расположить левую руку так, чтобы четыре вытянутых пальца указывали на направление движения положительных зарядов (направление тока), а магнитные линии входили в ладонь, «прокалывая» ее, то отставленный большой палец укажет направление действия силы Лоренца (или Ампера).

Например, если линии магнитного поля направлены сверху вниз, то руку надо располагать ладонью вверх. Теперь, если проводник с током направлен вперед и мы расположим четыре вытянутых пальца вперед, то отставленный большой палец укажет направление справа налево. Это и будет направление силы Ампера, действующей на данный проводник, или силы Лоренца, если двигаются заряды.

Правило левой руки

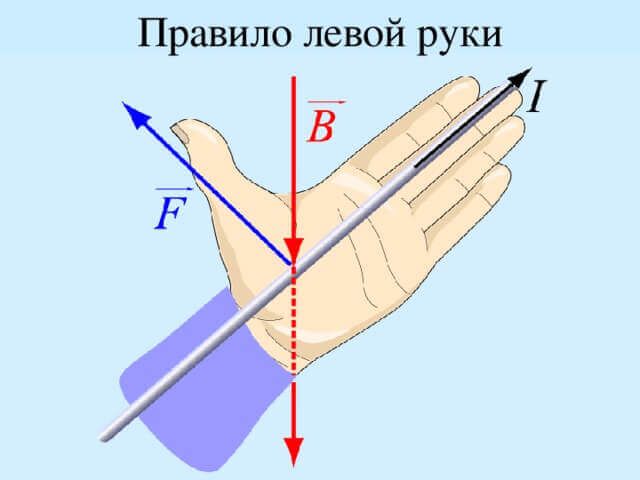
Как определить направление силы Лоренца

Направление силы Лоренца определяется по правилу левой руки (рис. 153):
если левую руку расположить так, чтобы перпендикулярная к скорости 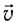Сила Лоренца - основные понятия, формулы и определение с примерами составляющая вектора индукции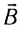
магнитного поля входила в ладонь, а четыре вытянутых пальца указывали направление движения положительно заряженной частицы, то отогнутый на 90° большой палец укажет направление силы Лоренца 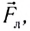Сила Лоренца - основные понятия, формулы и определение с примерами действующей на частицу со стороны магнитного поля. Для отрицательно заряженной частицы (например, для электрона) направление силы будет противоположным.

Будет интересно➡ Что такое короткое замыкание

Поскольку сила Лоренца перпендикулярна вектору скорости, то она не может изменить модуль скорости, а изменяет только ее направление и, следовательно, работы не совершает.

Таким образом, если поле однородно, то при движении частицы перпендикулярно к магнитной индукции поля ее траекторией будет окружность (рис. 154, а), плоскость которой перпендикулярна к магнитному полю.

Ускорение частицы 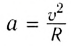Сила Лоренца - основные понятия, формулы и определение с примерами
(R — радиус окружности) направлено к центру окружности. Используя второй закон Ньютона, можем найти период обращения частицы по окружности
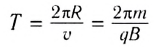
Сила Лоренца - основные понятия, формулы и определение с примерами

и радиус окружности

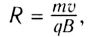
Сила Лоренца - основные понятия, формулы и определение с примерами
описываемой частицей в магнитном поле.

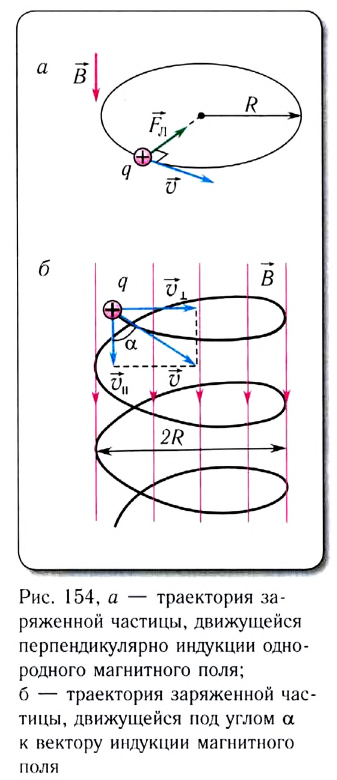
Сила Лоренца - основные понятия, формулы и определение с примерами

Если скорость направлена под углом к индукции магнитного поля, движение заряда можно представить в виде двух независимых движений (рис. 154, б):

равномерного вдоль поля со скоростью
(
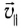
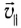
— составляющая вектора скорости, параллельная вектору индукции
магнитного поля);
по окружности радиусом R в плоскости, перпендикулярной к вектору
, с постоянной по модулю скоростью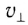
(
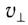
— составляющая вектора скорости, перпендикулярная вектору индукции
магнитного ноля).

В результате сложения обоих движений возникает движение по винтовой линии, ось которой параллельна магнитному полю (см. рис. 154, б). Период этого движения определяется по формуле
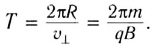
Сила Лоренца - основные понятия, формулы и определение с примерами

Действие силы Лоренца широко применяется в различных электротехнических устройствах:

электронно-лучевых трубках телевизоров и дисплеев;
ускорителях заряженных частиц (циклотронах);
масс-спектрометрах — приборах, определяющих отношение зарядов частиц к их массе по радиусу окружности, описываемой ими в магнитном поле;
магнитогидродинамических генераторах ЭДС (МГД-генератор — устройство для генерации электрических токов, использующее проводящие жидкости, движущиеся в магнитном поле).

Применение силы Лоренца

Практическое значение работ Лоренца мы можем наблюдать в электронно-лучевых трубках. Там поток электронов движется в магнитном поле, изменением которого задаётся траектория электронного пучка.

Данный принцип управления траекторией электронного пучка использовался в старых моделях телевизоров. Электроны под воздействием магнитных полей очерчивали линии на люминофоре кинескопа, рисуя изображения на экране.

Приведенное снизу соотношение представляет собой формулу угловой скорости движения заряженной частицы, происходящего по круговой траектории:

ω=υR=υqBmυ=qBm.

Оно носит название циклотронной частоты. Данная физическая величина не имеет зависимости от скорости частицы, из чего можно сделать вывод, что и от ее кинетической энергии она не зависит.

Данное обстоятельство находит свое применение в циклотронах, а именно в ускорителях тяжелых частиц (протонов, ионов).

Дуант – это полый металлический полуцилиндр, помещенный в вакуумную камеру между полюсами электромагнита в качестве одного из двух ускоряющих D-образного электрода в циклотроне.

К дуантам приложено переменное электрическое напряжение, чья частота эквивалентна циклотронной частоте. Частицы, несущие некоторый заряд, инжектируются в центре вакуумной камеры. В промежутке между дуантами они испытывают ускорение, вызываемое электрическим полем. Частицы, находящиеся внутри дуантов, в процессе движения по полуокружностям испытывают на себе действие силы Лоренца. Радиус полуокружностей возрастает с увеличением энергии частиц. Как и во всех других ускорителях, в циклотронах ускорение заряженной частицы достигается путем применения электрического поля, а ее удержание на траектории с помощью магнитного поля. Циклотроны дают возможность ускорять протоны до энергии, приближенной к 20 МэВ.

Однородные магнитные поля используются во многих устройствах самых разных типов назначений. В частности, они нашли свое применение так называемых масс-спектрометрах.

Масс-спектрометры – это такие устройства, использование которых позволяет нам измерять массы заряженных частиц, то есть ионов или ядер различных атомов.

Данные приборы используются для разделения изотопов (ядер атомов с одинаковым зарядом, но разными массами, к примеру, Ne20 и Ne22). Вылетающие из источника S ионы проходят через несколько малых отверстий, которые в совокупности формируют узкий пучок. После этого они попадают в селектор скоростей, где частицы движутся в скрещенных однородных электрическом, создающимся между пластинами плоского конденсатора, и магнитном, возникающим в зазоре между полюсами электромагнита, полях. Начальная скорость υ→ заряженных частиц направлена перпендикулярно векторам E→ и B→.

Будет интересно➡ История создания «лампочки Ильича»

Частица, которая движется в скрещенных магнитном и электрическом полях, испытывает на себе воздействия электрической силы qE→ и магнитной силы Лоренца. В условиях, когда выполняется E=υB, данные силы полностью компенсируют воздействие друг друга. В таком случае частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, которые движутся со скоростью υ=EB.

После данных процессов частицы с одинаковыми значениями скорости попадают в однородное магнитное поле B→ камеры масс-спектрометра. Частицы под действием силы Лоренца движутся в камере перпендикулярной магнитному полю плоскости. Их траектории представляют собой окружности с радиусами R=mυqB’. В процессе измерения радиусов траекторий при известных значениях υ и B’, мы имеем возможность определить отношение qm. В случае изотопов, то есть при условии q1=q2, масс-спектрометр может разделить частицы с разными массами.

С помощью современных масс-спектрометров мы имеем возможность измерять массы заряженных частиц с точностью, превышающей 10–4.

Рамка с током в магнитном поле

В листках по термодинамике мы говорили о важности циклически работающих машин: они снабжают нас энергией. Понимание законов термодинамики позволило сконструировать тепловые двигатели, которые исправно служат нам и по сей день.

Понимание же законов электромагнетизма дало возможность создать циклическую машину другого типа — электродвигатель.

Мы рассмотрим один из элементов электродвигателя — рамку с током в магнитном поле. Разобравшись в её поведении, мы сможем уловить основную идею функционирования электродвигателя.

Пусть прямоугольная рамка $1234$ может вращаться вокруг горизонтальной оси (рис. 4, слева). Рамка находится в вертикальном однородном магнитном поле $vec{B}$ . Ток течёт по рамке в направлении $1 > 2 > 3 > 4 > 1$

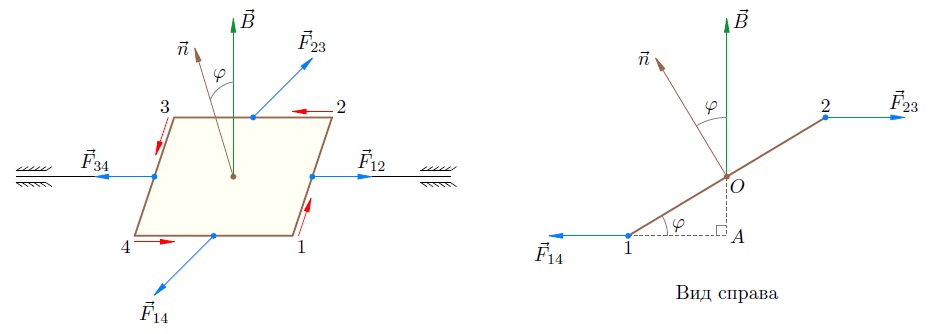
Сила Ампера и сила Лоренца

Рис. 4. Рамка с током в магнитном поле

Вектор $vec{n}$
называется вектором нормали; он перпендикулярен плоскости рамки и направлен туда, глядя откуда ток кажется циркулирующим против часовой стрелки. (Иными словами, вектор $vec{n}$
сонаправлен с вектором индукции магнитного поля, которое создаётся током в рамке.) Поворот рамки измеряется углом $alpha$ между векторами $vec{n}$ и $vec{B}$ .

Теперь определим направления сил Ампера, которые действуют на рамку со стороны магнитного поля. Эти силы расставлены на рисунке; вот вам ещё одно упражнение на правило часовой стрелки (левой руки) — обязательно проверьте правильность указанных направлений!

Силы $vec{F_{12}}$ и $vec{F_{34}}$ , приложенные к сторонам $12$ и $34$ , действуют вдоль оси вращения. Они лишь растягивают рамку и не вызывают её вращение.

Куда более интересны силы $vec{F_{23}}$ и $vec{F_{14}}$ , приложеные соответственно к сторонам $23$ и $14$ . Они лежат в горизонтальной плоскости и перпендикулярны оси вращения. Эти силы вращают рамку в направлении по часовой стрелке, если смотреть справа (рис. 4, правая часть). Вычислим момент этой пары сил относительно оси $O$
вращения рамки.

Пусть длина стороны $14$ равна $a$ Тогда

$F_{14} = F_{23} = IB_a.$

Пусть длина стороны $12$ равна $b$ . Плечо $d$ силы $F_{14}$ , как видно из рис. 4 (справа) равно:

$d=OA=frac{displaystyle b}{displaystyle 2 vphantom{1^a}} sin varphi$

Таким же будет плечо силы $vec{F_{23}}$ . Отсюда получаем момент сил, вращающий рамку:

$M=F_{14}d + F_{23}d=IB_a cdot frac{displaystyle b}{displaystyle 2 vphantom{1^a}} sin varphi + IB_a cdot frac{displaystyle b}{displaystyle 2 vphantom{1^a}} sin varphi=IBab sin varphi$

Теперь заметим, что $ab=S$ — площадь рамки. Окончательно имеем:

$M = IBS sin varphi.$
(3)

В этой формуле площадь служит единственной геометрической характеристикой рамки.Это наводит на мысль, что только площадь рамки и существенна в выражении для вращающего момента. И действительно, можно доказать (разбивая рамку на бесконечно узкие полоски, неотличимые от прямоугольников), что формула (3) справедлива для рамки любой формы с площадью $S$
.

Как видно из формулы (3), максимальный вращающий момент равен:

$M_{max} = IBS.$

Эта максимальная величина момента достигается при $varphi = frac{displaystyle pi}{displaystyle 2 vphantom{1^a}}$ , то есть когда плоскость рамки параллельна магнитному полю.

Вращающий момент становится равным нулю при $varphi = 0$ и $varphi = pi$ . Оба этих положения по-своему интересны.

При $varphi = pi$ плоскость рамки перпендикулярна полю, а векторы $n$ и $B$ направлены в разные стороны. Данное положение является положением неустойчивого равновенсия: стоит хоть немного шевельнуть рамку, как силы Ампера начнут её вращать в том же направлении, поворачивая вектор $vec{n}$ к вектору $vec{B}$ (убедитесь!).

При $varphi = 0$ плоскость рамки также перпендикулярна полю, а векторы $vec{n}$ и $vec{B}$
сонаправлены. Это — положение устойчивого равновенсия: при отклонении рамки возникает вращающий момент, стремящийся вернуть рамку назад (убедитесь!). Начнутся колебания рамки, постепенно затухающие из-за трения. В конце концов рамка остановится в положении $varphi = 0$ индукции внешнего магнитного поля (вот почему при намагничивании вещества элементарные токи ориентируются так, что их поля направлены в сторону внешнего магнитного поля). Полезное сопоставление: рамка занимает такое положение, что её положительная нормаль ориентируется в том же направлении, что и северный конец стрелки компаса, помещённой в это магнитное поле.

Будет интересно➡ Что такое коэффициент полезного действия (КПД) и как рассчитать его по формуле

Таким образом, поведение рамки в магнитном поле становится ясным: если отклонить рамку от положения устойчивого равновесия и отпустить, то рамка будет совершать колебания. С точки зрения совершения механической работы это не очень хорошо: если намотать нить на ось вращения и подвесить к нити груз, то груз будет то подниматься, то опускаться.
Но вот если исхитриться и заставить ток менять направление в нужные моменты, то вместо колебаний рамки начнётся её непрерывное вращение и, соответственно, непрерывный подъём подвешенного груза. Тогда-то и получится полноценный электродвигатель; идея с переменой направления тока реализуется с помощью коллектора и щёток.

Явление электромагнитной индукции, магнитный поток, поток магнитной индукции

Электромагнитная индукция: это явление возникновения электрического тока в проводящем контуре, который либо покоится в переменном магнитном поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется

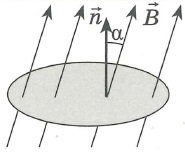
Магнитный поток (=поток магнитной индукции) [Вб]: через поверхность площадью S это величина равная произведению модуля вектора магнитной индукции В на площадь и косинус угла между вектром В и нормалью к плоскости S:
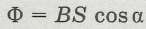
- при этом, очевидно, что если магнитная индукция перпендикулярна плоскости,
- то cos α = 1, и формула принимает вид:
  - Ф=BS

Явление электромагнитной индукции, магнитный поток, поток магнитной индукции

Примеры задач в физике, электротехнике

Задача № 1

Исходные данные для выполнения: длина проводника – 20 см, сила тока, протекающая в нем – 300 мА, угол между проводником и вектором магнитной индукции – 45о. Величина магнитной индукции – 0,5 Тл.

Требуется найти силу однородного магнитного поля, воздействующую на проводник.

Решение: необходимо применять основную формулу – Fa = B x I x L x sinα. Подставив нужные значения, получаем: Fa = 0,5 Тл х 0,3А х 0,2 м х (√2/2) = 0,03 Н.

Задача № 2

Исходные данные для решения: Проводник помещен в магнитное поле, индукция которого составляет 10 Тл. Сила действия магнитного поля перпендикулярна проводнику и составляет 20 Н. Сила тока, протекающего в проводнике – 5А.

Требуется вычислить длину отрезка проводника.

Решение: за основу берется формула Fa = B x I x L x sinα. Длина проводника определяется следующим образом: L = Fa/(B x I x sinα). Поскольку sinα = 1, получаем: L = Fa/(B x I). Остается подставить нужные значения и получить результат: L = 20Н/(10Тл х 5А) = 0,4 м.

Существуют аналогичные задачи с использованием силы Лоренца. Наглядно рассматрим два примера, которые решаются просто и понятно.

Задача № 3

Исходные данные для выполнения: в магнитном поле с индукцией 0,3 Тл передвигается заряд величиной 0,005 Кл со скоростью 200 м/с. Угол между направлением заряда и вектором магнитной индукции – 45º.

Определяется: величина силы, воздействующей на заряд.

Решение: используется основная формула FL = |q| x V x B x sinα. Подставляя исходные данные, получаем следующее: FL = 0,005Кл х 200м/с х 0,3Тл х sin 45о = (0,3 х √2)/2 = 0,21Н.

Задача № 4

Исходные данные для решения: заряженная частица величиной 0,5 мКл движется в магнитном поле с индукцией 2 Тл. Сила, действующая на заряд со стороны магнитного поля – 32 Н. Направление движения частицы и вектор магнитного поля расположены под углом 90º.

Требуется определить: скорость движения заряженной частицы.

Решение: изначально берется формула FL = |q| x V x B x sinα. Поскольку sinα = 1, она приобретает следующий вид: FL = |q| x V x B. Для определения скорости нужно: V = FL/(|q| x B). Остается вставить исходные данные: V = 32Н/(5*10-4Кл х 2Тл) = 32000 м/с.

ТеорияЗакон сохранения электрического заряда

ТеорияПочему в странах разные розетки?