Согласно закону Кулона, два точечных неподвижных заряда q1 и q2 в вакууме взаимодействуют между собой с силой, заданной формулой Fкл=((1/4)*π* ε)*(|q1|*|q2|/r2), где:
- Fкл – сила Кулона, Н;
- q1, q2 – модули зарядов, Кл;
- r – расстояние между зарядами, м;
- ε0 – электрическая постоянная, 8,85*10-12 Ф/м (Фарад на метр).
Если взаимодействие происходит не в вакууме, в формулу входит ещё одна величина, определяющая влияние вещества на силу Кулона, и запись закона Кулона выглядит так:
F=((1/4)*π* ε* ε)*(|q1|*|q2|/r2).
Эта величина обозначается греческой буквой ε (эпсилон), она безразмерна (не имеет единицы измерения). Диэлектрическая проницаемость является коэффициентом ослабления взаимодействия зарядов в веществе.
Часто в физике диэлектрическая проницаемость используется совместно с электрической постоянной, в этом случае удобно ввести понятие абсолютной диэлектрической проницаемости. Она обозначается εa и равна εa= ε* ε. В этом случае абсолютная проницаемость имеет размерность Ф/м. Обычную проницаемость ε также называют относительной, чтобы отличить ее от εa.
Простое объяснение
В повседневной жизни вы сталкиваетесь с различными веществами, такими как металлы, вода или кислород. Каждое из этих веществ по-разному реагирует на электрические поля.
Диэлектрическая проницаемость (диэлектрическая постоянная или абсолютная диэлектрическая проницаемость) ε описывает способность материала к поляризации электрическими полями и определяется следующим образом: ε = εr * ε0.
Здесь εr – относительная проницаемость, а ε0 – электрическая постоянная (или диэлектрическая проницаемость вакуума).
Если понимать значение термина “проницаемость” буквально, то это мера того, насколько сильно материя “пропускает” электрическое поле. Поэтому проницаемость можно рассматривать как меру того, насколько материя может быть поляризована.
Роль диэлектрической проницаемости воды в физике
Относительная диэлектрическая проницаемость ε среды, наряду с её относительной магнитной проницаемостью μ и удельной электропроводностью σ, влияет на распределение напряжённости электромагнитного поля в пространстве и используется при описании среды в системе уравнений Максвелла.
Среду со значениями μ=1и σ=0 называют идеальным диэлектриком (диэлектриком без поглощения, диэлектриком без потерь), для неё ε определяет такие вторичные параметры, как коэффициент преломления среды, скорость распространения, фазовую скорость и коэффициент укорочения длины электромагнитной волны в среде, волновое сопротивление среды.
Относительная диэлектрическая проницаемость реальных диэлектриков (диэлектриков с потерями, диэлектриков с поглощением, для которых σ>0 также влияет на значение тангенса угла диэлектрических потерь и коэффициент поглощения электромагнитной волны в среде.
Относительная диэлектрическая проницаемость среды влияет на электрическую ёмкость расположенных в ней проводников: увеличение ε приводит к увеличению ёмкости. При изменении ε в пространстве (то есть, если ε зависит от координат) говорят о неоднородной среде, зависимость ε от частоты электромагнитных колебаний — одна из возможных причин дисперсии электромагнитных волн, зависимость ε от напряженности электрического поля — одна из возможных причин нелинейности среды. Если среда является анизотропной, то в материальном уравнении ε будет не скаляром, а тензором. При использовании метода комплексных амплитуд в решении системы уравнений Максвелла и наличии потерь в среде (σ>0) оперируют комплексной диэлектрической проницаемостью.
Таким образом, ε является одним из важнейших «электромагнитных параметров» соответствующей среды.
Природа диэлектрической проницаемости воды
В основе природы диэлектрической проницаемости лежит явление поляризации под действием электрического поля. Большинство веществ в целом электрически нейтральны, хотя и содержат заряженные частицы. Эти частицы расположены в массе вещества хаотично и их электрические поля в среднем нейтрализуют друг друга.
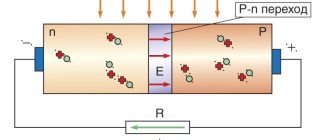
В диэлектриках находятся, в основном связанные заряды (их называют диполями). Эти диполи условно представляют собой связки из двух разноименных частиц, которые по толщине диэлектрика ориентированы спонтанно и в среднем создают нулевую напряженность электрического поля. Под действием внешнего поля диполи стремятся сориентироваться согласно приложенной силе. В результате создается дополнительное электрическое поле. Сходные явления происходят и в неполярных диэлектриках.
В проводниках процессы похожие, только там имеются свободные заряды, которые под действием внешнего поля разделяются и также создают собственное электрическое поле. Это поле направлено навстречу внешнему, экранирует заряды и снижает силу их взаимодействия. Чем больше способность вещества к поляризации, тем выше ε.
Практическое применение
Диэлектрическая проницаемость диэлектриков является одним из основных параметров при разработке электрических конденсаторов. Использование материалов с высокой диэлектрической проницаемостью позволяют существенно снизить физические размеры конденсаторов.
Параметр диэлектрической проницаемости учитывается при разработке печатных плат. Значение диэлектрической проницаемости вещества между слоями в сочетании с его толщиной влияет на величину естественной статической ёмкости слоев питания, а также существенно влияет на волновое сопротивление проводников на плате.
Эффект поляризации диэлектрика и проницаемость
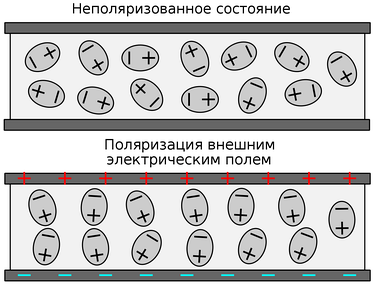
Схематическое изображение ориентации диполей в диэлектрической среде под воздействием электрического поля
Под воздействием электрического поля в диэлектрике происходит поляризация — явление, связанное с ограниченным смещением зарядов относительно положения равновесия без наложенного электрического поля или поворотом электрических диполей.
Это явление характеризует вектор электрической поляризации P,{displaystyle mathbf {P} ,}
равный дипольному моменту единицы объёма диэлектрика. В отсутствие внешнего поля диполи ориентированы хаотично (см. на рисунке сверху), за исключением особых случаев спонтанной поляризации в сегнетоэлектриках. При наличии поля диполи в большей или меньшей степени поворачиваются (на рисунке снизу), в зависимости от восприимчивости χ(ω){displaystyle chi (omega )}
конкретного материала, а восприимчивость, в свою очередь, определяет проницаемость ε(ω){displaystyle varepsilon (omega )}
.
Помимо дипольно-ориентационного, имеются и другие механизмы поляризации. Поляризация не изменяет суммарного заряда в любом макроскопическом объёме, однако она сопровождается появлением связанных электрических зарядов на поверхности диэлектрика и в местах неоднородностей материала. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле, как правило, направленное против внешнего наложенного поля. В итоге то, что εa≠ε0{displaystyle varepsilon _{a}neq varepsilon _{0}}
является следствием электрической поляризации материалов.
Измерение диэлектрической проницаемости воды
Относительная диэлектрическая проницаемость вещества ε{displaystyle varepsilon }
может быть определена путём сравнения ёмкости тестового конденсатора с данным диэлектриком (Cx{displaystyle C_{x}}
) и ёмкости того же конденсатора в вакууме (C0{displaystyle C_{0}}
):
ε=CxC0.{displaystyle varepsilon ={frac {C_{x}}{C_{0}}}.}
Cуществуют и оптические методы получения относительной диэлектрической проницаемости по коэффициенту преломления при помощи эллипсометров и рефрактометров.
Относительные диэлектрические проницаемости отдельных материалов
Наконец, мы приводим таблицу с типичными значениями относительной диэлектрической проницаемости (относительной диэлектрической проницаемости) различных материалов. Следует отметить, что в таких таблицах обычно указывается относительная проницаемость, а не сама абсолютная диэлектрическая проницаемость. Поэтому, если вы ищете таблицу для определения абсолютной диэлектрической проницаемости определенного материала, вы должны помнить, что приведенное там значение не является непосредственно той проницаемостью, которую вы ищете. Однако для заданного значения относительной проницаемости можно вычислить соответствующую абсолютную диэлектрическую проницаемость без особых дополнительных усилий. То есть нужно применять следующую уже известную нам формулу: ε = εr * ε0.
| Вещество | εr |
| Вакуум | ровно 1 |
| Гелий | 1,000065 |
| Медь | 5,6 |
| Воздух (сухой) | 1,00059 |
| Метанол | 32,6 |
| Бумага | 1 – 4 |
| Вода ( 20°C, 0 – 3 ГГц ) | 80 |
| Вода ( 0°C, 0 – 1 ГГц ) | 88 |
Таблица 1. Относительная диэлектрическая проницаемость выбранных веществ
(если не указано иное: при 18°C и 50 Гц)
В предыдущем разделе мы упоминали, что относительная проницаемость зависит, помимо прочего, от температуры и частоты. Поэтому важно знать и температуру, и частоту, если вы хотите получить значение из таблицы. Например, относительная проницаемость воды при температуре 20°C и частоте 0 ГГц равна 80. Если температура 0°C, а частота та же, относительная проницаемость воды равна 88. Медь, с другой стороны, имеет относительную проницаемость 5,6. Это означает, что вода как среда уменьшит напряжение на конденсаторе в 80 раз, в то время как медь уменьшит его только в 5,6 раз.
Диэлектрические свойства воды и льда
Численная модель диэлектрических свойств льда позволяет осуществить расчет показателя преломления и показателя поглощения электромагнитных волн в диапазоне частот от 0 до 6.7·1015 Гц.
В диапазоне частот от 0 до 3.49·107 Гц значения относительной диэлектрической проницаемости рассчитываются с помощью теории Дебая, в диапазоне от 3.49·107 до 6.66·1015 Гц – по табличным данным, полученным в результате натурных экспериментов. В диапазоне температур от 233 до 273 К (от -40 до 0 °С) относительная ошибка расчета по формуле не превышает 1.5 %.
В диапазоне температур от 233 до 273 К (от -40 до 0 °С) относительная ошибка расчета по формуле не превышает 1.5 %.
В диапазоне частот электромагнитного излучения от 3.49·107 до 6.66·1015 Гц модель возвращает значение, полученное путем интерполяции табличных данных о показателях преломления и поглощения льда. Табличные данные соответствуют диапазону температуры от 213.16 до 272.16 K (от -60 до -1 °C).
Для целей обеспечения гладкости функций действительной и мнимой частей относительной диэлектрической проницаемости льда на частоте 3.49·107 Гц (для льда), где стыкуется модель Дебая и табличные данные, используются следующие уточняющие формулы для относительной диэлектрической проницаемости в статическом пределе.
Результаты численного расчета значений относительной диэлектрической проницаемости льда в зависимости от частоты электромагнитного излучения при двух значениях температуры представлены в таблице. На рисунках 1 – 4 представлены результаты расчета зависимости от частоты электромагнитных волн показателя преломления, показателя поглощения, действительной части комплексной диэлектрической проницаемости, мнимой части комплексной диэлектрической проницаемости воды и льда.
Предыдущая