Согласно закону Кулона, два точечных неподвижных заряда q1 и q2 в вакууме взаимодействуют между собой с силой, заданной формулой Fкл=((1/4)*π* ε)*(|q1|*|q2|/r2), где:
- Fкл – сила Кулона, Н;
- q1, q2 – модули зарядов, Кл;
- r – расстояние между зарядами, м;
- ε0 – электрическая постоянная, 8,85*10-12 Ф/м (Фарад на метр).
Если взаимодействие происходит не в вакууме, в формулу входит ещё одна величина, определяющая влияние вещества на силу Кулона, и запись закона Кулона выглядит так:
F=((1/4)*π* ε* ε)*(|q1|*|q2|/r2).
Эта величина обозначается греческой буквой ε (эпсилон), она безразмерна (не имеет единицы измерения). Диэлектрическая проницаемость является коэффициентом ослабления взаимодействия зарядов в веществе.
Часто в физике диэлектрическая проницаемость используется совместно с электрической постоянной, в этом случае удобно ввести понятие абсолютной диэлектрической проницаемости. Она обозначается εa и равна εa= ε* ε. В этом случае абсолютная проницаемость имеет размерность Ф/м. Обычную проницаемость ε также называют относительной, чтобы отличить ее от εa.
Простое объяснение
В повседневной жизни вы сталкиваетесь с различными веществами, такими как металлы, вода или кислород. Каждое из этих веществ по-разному реагирует на электрические поля.
Диэлектрическая проницаемость (диэлектрическая постоянная или абсолютная диэлектрическая проницаемость) ε описывает способность материала к поляризации электрическими полями и определяется следующим образом: ε = εr * ε0.
Здесь εr – относительная проницаемость, а ε0 – электрическая постоянная (или диэлектрическая проницаемость вакуума).
Если понимать значение термина “проницаемость” буквально, то это мера того, насколько сильно материя “пропускает” электрическое поле. Поэтому проницаемость можно рассматривать как меру того, насколько материя может быть поляризована.
Некоторые свойства
Вообще говоря, диэлектрическая проницаемость является тензором, определяемым из следующих соотношений (в записи использовано соглашение Эйнштейна):

или

здесь:

— вектор напряжённости электрического поля,
— вектор электрической индукции,
— тензор абсолютной диэлектрической проницаемости.
Для среды с конечной проводимостью (поглощающая среда) в тензор диэлектрической проницаемости часто включают мнимую компоненту, пропорциональную проводимости. Пусть электрическое поле колеблется по гармоническому закону (здесь 
— мнимая единица):

Тогда одно из уравнений Максвелла для непроводящей среды с постоянной во времени  :
:

С другой стороны, для проводящей среды с тензором проводимости  :
:

Чтобы привести это уравнение к виду, формально совпадающему с видом уравнения для непроводящей среды, можно ввести комплексную диэлектрическую проницаемость  :
:

Таким образом, становится возможным использование для проводящих сред формул, полученных для идеальных диэлектриков. Кроме того, даже в случаях, когда в постоянном поле среда обладает очень малой проводимостью, на высоких частотах могут появиться потери, которые при таком подходе также можно приписать некоторой «эффективной» проводимости. В таком случае говорят о тангенсе угла диэлектрических потерь:

В некоторых случаях колебания электрического поля изначально определяются как  .
.
Необходимо отметить, что:
- Приведенные выше формулы пригодны только для линейных (в электрическом отношении) сред. При небольших напряжённостях полей отклонения от линейности в подавляющем большинстве случаев пренебрежимо малы.
- В электрически изотропных (одинаковых во всех направлениях) средах

, где δij — символ Кронекера, поэтому уравнения Максвелла чаще всего записываются с использованием скалярных диэлектрических проницаемостей. В том числе, для вакуума
считается равной
. - Сами по себе

и
обычно зависят от частоты электрического поля. - На микроскопическом уровне средой всегда является вакуум, а условие

является следствием электрической поляризации материалов.
Зависимость от частоты
Следует отметить, что диэлектрическая проницаемость в значительной степени зависит от частоты электромагнитного поля. Это следует всегда учитывать, поскольку таблицы справочников обычно содержат данные для статического поля или малых частот вплоть до нескольких единиц кГц без указания данного факта. В то же время существуют и оптические методы получения относительной диэлектрической проницаемости по коэффициенту преломления при помощи эллипсометров и рефрактометров. Полученное оптическим методом (частота 1014 Гц) значение будет значительно отличаться от данных в таблицах.
Рассмотрим, например, случай воды. В случае статического поля относительная диэлектрическая проницаемость воды приблизительно равна 80. Это имеет место вплоть до инфракрасных частот. Начиная примерно с 2 ГГц εr начинает падать. В оптическом диапазоне εr составляет приблизительно 1,77, соответственно показатель преломления воды равен 1,33.
Роль диэлектрической проницаемости среды в физике
Относительная диэлектрическая проницаемость ε среды, наряду с её относительной магнитной проницаемостью μ и удельной электропроводностью σ, влияет на распределение напряжённости электромагнитного поля в пространстве и используется при описании среды в системе уравнений Максвелла.
Среду со значениями μ=1 и σ=0 называют идеальным диэлектриком (диэлектриком без поглощения, диэлектриком без потерь), для неё ε определяет такие вторичные параметры, как коэффициент преломления среды, скорость распространения, фазовую скорость и коэффициент укорочения длины электромагнитной волны в среде, волновое сопротивление среды.
Относительная диэлектрическая проницаемость реальных диэлектриков (диэлектриков с потерями, диэлектриков с поглощением, для которых σ>0) также влияет на значение тангенса угла диэлектрических потерь и коэффициент поглощения электромагнитной волны в среде.
Относительная диэлектрическая проницаемость среды влияет на электрическую ёмкость расположенных в ней проводников: увеличение ε приводит к увеличению ёмкости. При изменении ε в пространстве (то есть, если ε зависит от координат) говорят о неоднородной среде, зависимость ε от частоты электромагнитных колебаний — одна из возможных причин дисперсии электромагнитных волн, зависимость ε от напряженности электрического поля — одна из возможных причин нелинейности среды. Если среда является анизотропной, то в материальном уравнении ε будет не скаляром, а тензором. При использовании метода комплексных амплитуд в решении системы уравнений Максвелла и наличии потерь в среде (σ>0) оперируют комплексной диэлектрической проницаемостью.
Таким образом, ε является одним из важнейших «электромагнитных параметров» соответствующей среды.
Практическое применение
Диэлектрическая проницаемость диэлектриков является одним из основных параметров при разработке электрических конденсаторов. Использование материалов с высокой диэлектрической проницаемостью позволяют существенно снизить физические размеры конденсаторов.
Ёмкость конденсаторов определяется:

где εr — относительная диэлектрическая проницаемость вещества между обкладками, εо — электрическая постоянная, S — площадь обкладок конденсатора, d — расстояние между обкладками.
Параметр диэлектрической проницаемости учитывается при разработке печатных плат. Значение диэлектрической проницаемости вещества между слоями в сочетании с его толщиной влияет на величину естественной статической ёмкости слоев питания, а также существенно влияет на волновое сопротивление проводников на плате.
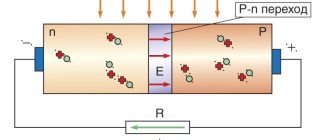
Эффект поляризации диэлектрика и проницаемость

Схематическое изображение ориентации диполей в диэлектрической среде под воздействием электрического поля
Под воздействием электрического поля в диэлектрике происходит поляризация — явление, связанное с ограниченным смещением зарядов относительно положения равновесия без наложенного электрического поля или поворотом электрических диполей.
Это явление характеризует вектор электрической поляризации P, равный дипольному моменту единицы объёма диэлектрика. В отсутствие внешнего поля диполи ориентированы хаотично (см. на рисунке сверху), за исключением особых случаев спонтанной поляризации в сегнетоэлектриках. При наличии поля диполи в большей или меньшей степени поворачиваются (на рисунке снизу), в зависимости от восприимчивости χ(ω) конкретного материала, а восприимчивость, в свою очередь, определяет проницаемость ε(ω).
Помимо дипольно-ориентационного, имеются и другие механизмы поляризации. Поляризация не изменяет суммарного заряда в любом макроскопическом объёме, однако она сопровождается появлением связанных электрических зарядов на поверхности диэлектрика и в местах неоднородностей материала. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле, как правило, направленное против внешнего наложенного поля. В итоге то, что εa≠ε0 является следствием электрической поляризации материалов.
Диэлектрическая проницаемость непоглощающей среды
Проницаемость и связанные с ней величины
Применительно к диэлектрической среде без потерь справедливы соотношения:
D=ε0E+P=ε0(1+χ)E=ε0εE
В большинстве случаев χ и, соответственно, ε — это просто безразмерные константы конкретного материала. В вакууме χ равно нулю.
Особая ситуация возникает для нелинейных сред, когда ε зависит от величины поля E; такое возможно в сравнительно сильных полях. В сегнетоэлектриках возможно появление спонтанной поляризации, а именно сохранение поляризации P≠0 после снятия ранее наложенного внешнего поля.
Распределение электрического поля в пространстве с различными диэлектриками находится из численного решения уравнения Максвелла:
∇⋅D(r)=ρ(r), или уравнения Пуассона для электрического потенциала φ: ∇(ε(r)∇φ(r))=−ε0−1ρ(r), обозначает плотность свободных зарядов.
На незаряженной границе двух диэлектрических сред отношение нормальных компонент напряжённости поля En с обеих сторон равно обратному отношению значений проницаемости сред.
В случае однородного диэлектрика его наличие приводит к снижению электрического поля E(r) в ε раз, по сравнению со случаем вакуума при том же распределении свободных зарядов. Помимо закона Кулона, практически важным примером является конденсатор любой геометрии, заряд (но не разность потенциалов) обкладок которого фиксирован.
Проницаемость в оптическом диапазоне частот
Диэлектрическая проницаемость, совместно с магнитной, определяют фазовую скорость распространения электромагнитной волны в рассматриваемой среде, а именно:
ε0ε(ω)μ0μ(ω)=vph−2.
Показатель преломления диэлектрика без потерь можно выразить как квадратный корень из произведения его магнитной и диэлектрической проницаемостей:
n(ω)=μ(ω)⋅ε(ω).
Для немагнитных сред μ=1. Значения ε для существенного в конкретном контексте оптического диапазона могут очень сильно отличаться от статических значений: как правило, ε намного ниже, чем для статического поля.
Однако, если рассматривать оптический диапазон частот сам по себе, то в нём с ростом ω величина ε (а значит, и n) чаще всего возрастает. Такое поведение показателя преломления («синий свет преломляется сильнее красного») является случаем так называемой нормальной дисперсии. Противоположную ситуацию аномальную дисперсию можно наблюдать вблизи полос поглощения, но такой случай не может рассматриваться как случай без диссипативных потерь.
Тензор проницаемости анизотропных сред
Диэлектрическая проницаемость связывает электрическую индукцию D и напряжённость электрического поля E.
В электрически анизотропных средах компонента вектора напряжённости Ei может не только влиять на ту же самую компоненту вектора электрической индукции Di, но и порождать другие его компоненты Dj(j≠i).
В общем случае проницаемость является тензором, определяемым из следующего соотношения (в записи использовано соглашение Эйнштейна):
Di=ε0εijEj, или, иначе: D=εaE, где жирный шрифт использован для векторных и тензорных величин, а
E=E1e1+E2e2+E3e3 — вектор напряжённости электрического поля,
D=D1e1+D2e2+D3e3 — вектор электрической индукции,εa=ε0εij — тензор абсолютной диэлектрической проницаемости.
В изотропном случае любая компонента вектора напряженности Ei влияет только на Di, при этом εij= δijεгде δij символ Кронекера, поэтому уравнения Максвелла могут быть записаны с использованием скалярной диэлектрической проницаемости просто коэффициент в уравнении).
Проницаемость диэлектрической среды с потерями [ править | править код ]
Комплексная диэлектрическая проницаемость
При описании колебаний электрического поля методом комплексных амплитуд в случае диэлектрической среды с конечной проводимостью σ{displaystyle sigma }
уравнения Максвелла можно записывать по аналогии со случаем идеального диэлектрика, если ввести мнимую компоненту проницаемости.
Пусть напряженность электрического поля изменяется во времени по гармоническому закону (далее i{displaystyle i}
— мнимая единица):
E=E0e−iωt.
Тогда ∂E/∂t=−iωE, а уравнение Максвелла для магнитного поля применительно к проводящей среде выглядит:
∇×H=j+∂D∂t=σE+ε0ε∂E∂t=ε0(ε+iσε0ω)∂E∂t
Чтобы привести это уравнение к виду, формально совпадающему с видом уравнения для непроводящей среды, величина, стоящая в скобках, интерпретируется как комплексная диэлектрическая проницаемость ε^.
Значок сверху (опускаемый, если это не влечёт двусмысленности) подчеркивает, что речь идёт о комплексной величине. При наличии анизотропии ε^ становится тензорной величиной. Иногда в методе комплексных амплитуд используют зависимость вида E=E0eiωt — тогда знак перед i должен быть заменён везде.
Даже в случаях, когда в постоянном электрическом поле среда обладает очень малой проводимостью, на высоких частотах могут проявиться существенные потери, которые при таком подходе приписываются некоторой «эффективной» диэлектрической проницаемости:
ε^=ε′+iε″.
Наличие мнимой части связано с конечной проводимостью σ, которая и обусловливает поглощение. Если частота изменения поля составляет ω, то ε″=σ/ε0ω.
Без метода комплексных амплитуд подставлять комплексную ε^в уравнения Максвелла нельзя (следует оперировать непосредственно ε и σ). Однако если известны ε′ и ε″, то можно воспользоваться ими для анализа свойств среды, вычисления ряда других параметров включая показатель поглощения, а также получить готовыми ε=ε′ и σ=ε0|ε″|⋅ω для соответствующей частоты.
Характеристика диэлектрических потерь
Плотность мощности (Ватт/м3) тепловыделения за счёт диэлектрических потерь составляет:
wloss=WlossV=ω⋅ε0⋅|ε″|⋅E2.
Подобный механизм разогрева широко используется в микроволновых печах. Для характеристики диэлектрика с поглощением также используется величина «тангенса угла потерь» — отношение мнимой и вещественной частей комплексной диэлектрической проницаемости:
tgδ=|ε″|ε′=σωε0ε′.
При протекании переменного тока через конденсатор векторы напряжения и тока сдвинуты на угол π/2−δ, где δ — угол диэлектрических потерь.
При отсутствии потерь δ = 0. Тангенс угла потерь определяется отношением активной мощности к реактивной при синусоидальном напряжении заданной частоты. Величина, обратная tg δ, называется добротностью конденсатора.
При наличии поглощения взаимосвязь между компонентами комплексной проницаемости и оптическими величинами (показателями преломления и поглощения) устанавливается с использованием соотношений Крамерса — Кронига и имеет вид:
(n+ik)2=(ε′+iε″)μ,
откуда для немагнитных сред следует:
n2=12⋅(ε′2+ε′′2+ε′),
k2=12⋅(ε′2+ε′′2−ε′).
Типичная частотная зависимость проницаемости
![Типичное поведение вещественной и мнимой составляющих диэлектрической проницаемости в широком диапазоне частот. Области резкого изменения этих составляющих соответствуют линиям поглощения, которые могут иметь различную природу: дипольная или ионная релаксация, атомные и электронные резонансы на высоких частотах[9]. СВЧ — сверхвысокие частоты, ИК — инфракрасный диапазон, ВД — видимый диапазон, УФ — ультрафиолетовый диапазон.](https://electroinfo.net/images/wikipedia/commons/thumb/9/97/Dielectric_responses-ru.svg/im324-553px-Dielectric_responses-ru.svg.png)
Типичное поведение вещественной и мнимой составляющих диэлектрической проницаемости в широком диапазоне частот. Области резкого изменения этих составляющих соответствуют линиям поглощения, которые могут иметь различную природу: дипольная или ионная релаксация, атомные и электронные резонансы на высоких частотах [9] . СВЧ — сверхвысокие частоты, ИК — инфракрасный диапазон, ВД — видимый диапазон, УФ — ультрафиолетовый диапазон.
Зависимость действительной и мнимой составляющих диэлектрической проницаемости воды при 20 °C
Параметры ε′ и σ обычно сильно зависят от частоты колебаний напряженности электрического поля. Например, ясно, что в дипольной модели поляризации процесс ориентации диполей может не успевать следовать за изменениями приложенного поля, что может проявиться как возрастанием, так и снижением проницаемости по сравнению с её статическим значением.
Наиболее типичное поведение ε′ и ε″как функций частоты ω представлено на рисунке. Далеко от линий и полос поглощения («собственных частот») материала значения ε″ малы, а ε′ не изменяется или слабо растёт с частотой. В областях вблизи линий компонента ε″ имеет максимумы, а ε′ резко спадает. При этом не исключена ситуация, при которой ε′(ω) в каком-то диапазоне окажется отрицательным или положительным, но меньше единицы. Практически ε′<0 является редким случаем, а ситуация 0<ε′(ω)<1 на предельно высоких (рентгеновских) частотах характерна для всех материалов: в этой области ε′’с ростом ω подходит к единице снизу.
Таблицы неспециализированных справочников обычно содержат данные для статического поля или малых частот вплоть до нескольких единиц кГц (иногда даже без указания данного факта). В то же время значения ε′ в оптическом диапазоне (частота 1014 Гц) намного отличаются в меньшую сторону от данных, представленных в подобных таблицах. Например для воды в случае статического поля относительная диэлектрическая проницаемость приблизительно равна 80. Это имеет место вплоть до инфракрасных частот. Начиная примерно с 2 ГГц ε (здесь ε′≈ε) начинает падать. В оптическом диапазоне εсоставляет около 1,77, соответственно показатель преломления воды равен 1,33, а не квадратному корню из восьмидесяти.
Измерение
Относительная диэлектрическая проницаемость вещества εr может быть определена путем сравнения ёмкости тестового конденсатора с данным диэлектриком (Cx) и ёмкости того же конденсатора в вакууме (Co):

Значения диэлектрической проницаемости для некоторых веществ [
ВеществоХимическая формулаУсловия измеренияХарактерное значение εr
| Вакуум | – | – | 1 | |
| Воздух | – | Нормальные условия, 0,9 МГц | 1,00058986 ± 0,00000050 | |
| Углекислый газ | CO2 | Нормальные условия | 1,0009 | |
| Тефлон | – | – | 2,1 | |
| Нейлон | – | – | 3,2 | |
| Полиэтилен | [-СН2-СН2-]n | – | 2,25 | |
| Полистирол | [-СН2-С(С6Н5)Н-]n | – | 2,4-2,7 | |
| Каучук | – | – | 2,4 | |
| Битум | – | – | 2,5-3,0 | |
| Сероуглерод | CS2 | – | 2,6 | |
| Парафин | С18Н38 − С35Н72 | – | 2,0-3,0 | |
| Бумага | – | – | 2,0-3,5 | |
| Электроактивные полимеры | − | − | 2-12 | |
| Эбонит | (C6H9S)2 | − | 2,5-3,0 | |
| Плексиглас (оргстекло) | – | – | 3,5 | |
| Кварц | SiO2 | – | 3,5-4,5 | |
| Диоксид кремния | SiO2 | − | 3,9 | |
| Бакелит | – | – | 4,5 | |
| Бетон | − | − | 4,5 | |
| Фарфор | − | − | 4,5-4,7 | |
| Стекло | − | − | 4,7 (3,7-10) | |
| Стеклотекстолит FR-4 | – | – | 4,5-5,2 | |
| Гетинакс | – | – | 5-6 | |
| Слюда | – | – | 7,5 | |
| Резина | − | − | 7 | |
| Поликор | 98 % Al2O3 | – | 9,7 | |
| Алмаз | − | − | 5,5-10 | |
| Поваренная соль | NaCl | − | 3-15 | |
| Графит | C | − | 10-15 | |
| Керамика | − | − | 10-20 | |
| Кремний | Si | − | 11.68 | |
| Бор | B | − | 2.01 | |
| Аммиак | NH3 | 20 °C | 17 | |
| 0 °C | 20 | |||
| −40 °C | 22 | |||
| −80 °C | 26 | |||
| Спирт этиловый | C2H5OH или CH3-CH2-OH | − | 27 | |
| Метанол | CH3OH | − | 30 | |
| Этиленгликоль | HO—CH2—CH2—OH | − | 37 | |
| Фурфурол | C5H4O2 | − | 42 | |
| Глицерин | HOCH2CH(OH)-CH2OH или C3H5(OH)3 | 0 °C | 41,2 | |
| 20 °C | 47 | |||
| 25 °C | 42,5 | |||
| Вода | H2O | 200 °C | 34,5 | |
| 100 °C | 55,3 | |||
| 20 °C | 81 | |||
| 0 °C | 88 | |||
| Плавиковая кислота | HF | 0 °C | 83,6 | |
| Формамид | HCONH2 | 20 °C | 84 | |
| Серная кислота | H2SO4 | 20-25 °C | 84-100 | |
| Пероксид водорода | H2O2 | −30 °C — +25 °C | 128 | |
| Синильная кислота | HCN | (0-21 °C) | 158 | |
| Двуокись титана | TiO2 | – | 86-173 | |
| Титанат кальция | CaTiO3 | – | 170 | |
| Титанат стронция | SrTiO3 | – | 310 | |
| Титанат бария-стронция | (Ba1−xSrx)TiO3, 0<> | – | 500 | |
| Титанат бария | BaTiO3 | (20-120 °C) | 1250-10000 | |
| Цирконат-титанат свинца | (Pb[ZrxTi1-x]O3, 0<> | 500-6000 | ||
| Сополимеры | – | – | до 100000 | |
| Сульфид кадмия | CdS | 9,3 |