Основные принципы
Любая электротехническая цепь состоит из участков (ветвей), образующих узлы и контуры. Для определения значений тока через любой элемент используют два закона Кирхгофа. Прямое составление уравнений дает систему с их максимальным количеством, равным количеству ветвей. В результате, если множество узлов цепи равно У, а число ветвей Р, то уравнения распределяются следующим образом:
- Для узлов У-1 по закону Кирхгофа для токов;
- Для ветвей Р-У+1 по закону Кирхгофа для напряжений.
Данное количество избыточно и приводит к образованию громоздкой системы уравнений большой размерности.
Для упрощения расчетов разработаны методики, которые позволяют сократить количество уравнений до приемлемых значений без снижения точности результатов. Наиболее простым является метод контурных токов.
Определение и суть метода контурных токов
Векторная диаграмма токов и напряжений
По данному методу в исследуемой цепи выделяются независимые плоские замкнутые контуры, включающие все, без исключения, элементы. Предполагается, что в каждом контуре может протекать некоторый контурный ток. В том случае, если цепь с элементом принадлежит только одному контуру, то ток через входящие в нее элементы равен контурному. Если элемент охватывается несколькими контурами, то он в ней равен алгебраической (с учетом направления) сумме контурных токов.
Разбиение цепи на контуры
Важно! Суммирование должно производиться строго с учетом направления движения при обходе контура. Знак «плюс» – при совпадении направления, «минус» – при противоположном.
При составлении уравнений учитываются входящие в схему источники ЭДС и тока.
На практике удобнее преобразовать идеальный источник тока в идеальный источник ЭДС. Преобразование выполняется согласно закона Ома:
U=I∙r, где r – внутреннее сопротивление источника тока (напряжения).
Методика расчета используется как в цепях постоянного, так и переменного напряжения. При расчетах цепей переменного напряжения с реактивными элементами используются комплексные величины, затем вычисляются мгновенные и амплитудные величины токов и напряжений и углы сдвига фаз между ними.
Цепь с реактивными элементами
Термины, определения и главная идея МКТ
Для расчетов реальных (действительных) значений токов в МКТ было введено дополнительное понятие о фиктивной (виртуальной) величине, названной контурным током (КТ), протекающим (гипотетически) в каждом независимом контуре. КТ имеет одно и то же значение в ветвях данного контура.
КТ вычисляются с помощью решения уравнений, которые формируются согласно ВПК для всех независимых контуров. Искомые значения токов в ветвях вычисляются простым сложением полученных величин КТ со знаком «плюс» или «минус» в зависимости от направления.
Расчёт действительных токов в электрических цепях с помощью МКТ производится в следующей последовательности:
- Проектируется (рисуется) принципиальная электрическая схема.
- Фиксируются все самостоятельные контуры.
- Задаётся (обозначается) направленность каждого КТ (по часовой стрелке либо наоборот). Для обозначения и нумерации КТ используются двойные индексы, например, I11, I22, I33 …
- Для каждого контура, согласно ВПК, пишется уравнение, где неизвестным параметром является соответствующий ток IKK. В уравнения должны быть учтены присутствующие цепи источники тока и ЭДС.
- В совпадающих ветвях, принадлежащих двум соседствующим контурам, протекают два КТ. Поэтому вклад в падение напряжения на нагрузках в подобных ветвях будут вносить оба тока, что должно быть отражено в уравнении.
- Далее полученный набор уравнений (система) решается с помощью того или иного математического алгоритма. В результате получаем все значения КТ.
- Вводятся обозначения реальных токов ветвей и задаются их действительные направления. Во избежание путаницы можно использовать, например, такие буквы и индексы: J1, J2, J3 или J1, J2, J3.
- Используя найденные величины КТ, вычисляем искомые токи, которые равны алгебраическим (с учётом знаков) суммам КТ.
- При суммировании следует учитывать, что КТ, совпадающий по направлению с настоящим током, прибавляется «плюсом», а несовпадающий — с «минусом».
Способы построения контуров
Тщательное обозначение контуров позволяет задать минимальный набор КТ. Любой элемент схемы должен быть представлен хотя в одном контуре. При построении используются два основных метода:
- планарных графов;
- выделения максимального дерева.
Использование планарных графов
Метод планарных графов применяется при ручном расчете, поскольку он наиболее прост и нагляден. Для построения плоского графа схему рисуют таким образом, чтобы не было взаимного пересечения ветвей. Получается, что схему можно разбить на несколько ограниченных участков, которые образуют контуры.
Рассматриваемая методика неприменима без дополнительных преобразований, если невозможно выразить схему в виде планарного графа.
Выделение максимального дерева
Данный математический метод разработан для компьютерных расчётов с помощью соответствующего программного обеспечения. Основная идея метода состоит в изъятии отдельных ветвей в соответствии с жёстким алгоритмом:
- На каждом этапе может быть изъято не более одной ветви.
- Изъятие не должно разбивать граф на отдельные куски или приводить к «зависшим узлам».
- Число исключённых звеньев должно быть эквивалентно числу независимых контуров.
- Подключение ранее изъятой ветви формирует соответствующий контур.
Последовательность расчёта по методу контурных токов
Расчет цепей по методу контурных токов рекомендуется вести в следующей последовательности.
- Упростить исходную цепь, заменив реальные источники тока на реальные источники напряжения.
- Выбрать независимые контуры, направление контурных токов в них и направления токов в ветвях, входящих только в один контур должны совпадать с направлением контурного тока.
- Записать и решить стандартную систему уравнений по методу контурных токов.
- По найденным контурным токам найти по первому закону Кирхгофа токи в остальных ветвях схемы.
- Выполнить проверку результатов расчёта.
Если в схеме идеальные источники тока и их не преобразовали в модели с источниками ЭДС, расчет имеет ряд особенностей. Чтобы выбрать независимые контуры, необходимо использовать дерево графа так, чтобы в идеальные источники тока входили в ветви соединения. В этом случае токи источников тока приравниваем к известным контурным токам, а уравления составляют и решают только для контуров с неизвестными контурными токами. При этом в уравнения включаются слагаемые, которые приравняли токам идеальных источников тока.
Оптимизированная процедура составления системы
По упрощенной методике поступают следующим образом:
- В уравнениях в левой части записывают произведение суммы всех входящих в контур сопротивлений на контурный ток;
- От полученного выражения вычитаются умноженные на сумму сопротивлений общей ветви соседние контурные токи;
- Справа записывается сумма источников ЭДС контура.
Формальный подход
Система уравнений для МКТ, записанная в матричном представлении, называется формальным подходом. Для расчётов необходимы следующие матрицы:
- С — состоит из i строк и j столбцов, где i — число строк, j — число столбцов;
- Z — диагональная матрица сопротивлений, число строк и столбцов равно числу ветвей;
- Сt — транспонированная С-матрица. В транспонированной матрице строки и столбцы меняются местами;
- I — матрица КТ (состоит из одного столбца);
- J — матрица-столбец — источники тока;
- E — матрица-столбец, содержащая ЭДС-источники с тем или иным знаком.
Окончательное уравнение для расчётов в матричном представлении имеет следующий вид:
С * Z * Сt * I = С * (E + Z * J)
Пример системы уравнений
Ниже рассмотрен пример расчета конкретной схемы без учета номиналов элементов.
Пример решения
В заданной цепи выделяют три контура. Как выразить токи в ветвях через контурные:
- i1=I1;
- i2=I2;
- i3=I3;
- i4=I2+I3;
- i5=I1+I2;
- i6=I1-I3.
Как составить систему уравнений:
- i1R1+i5R5+i6R6=E1;
- i2R2+i4R4+i5R5=E2;
- i3R3+i4R4-i6R6=0
Как подставитьконтурныезначения:
- I1R1+( I1+I2)R5+( I1-I3)R6=E1;
- I2R2+( I2+I3)R4+( I1+I2)R5=E2;
- I3R3+( I2+I3)R4-( I1-I3)R6=0
После преобразования получается необходимая система уравнений:
- (R1+R5+R6)I1+R5I2+R6I3=E1;
- R5I1+(R2+R4+R5)I2+R4I3=E2;
- -R6I1+R4I2+(R3+R4+R6)I3=0.
Система из трех уравнений легко решается после подстановки известных параметров. Из полученных значений контурных токов затем можно найти искомые величины.
Данный пример решения задач по методу контурных токов показывает, что любую достаточно сложную схему можно существенно упростить для решения, руководствуясь указаниями.
Важно! Метод неприменим, если нет возможности преобразовать цепь без взаимного пересечения ветвей.
В некоторых случаях упростить схему можно путем преобразования ветвей, соединенных по схеме «звезда» в треугольник.
Точно такие же результаты получаются при использовании метода узловых потенциалов. В основе расчетов – поиск потенциала каждого узла (так называемый узловой потенциал). Существуют программы, позволяющие произвести онлайн расчет параметров по рассмотренным методам.
Рассчитайте схему цепи
Выполните расчет цепи постоянного тока или сохраните схему цепи, чтобы потом была возможность начать с того места, на чем закончили (для этого воспользуйтесь кнопками, расположенными ниже ‘Рассчитать схему’ или ‘Сохранить схему’).
Добавьте элементы в цепь
| Проводник – горизонтальный Проводник – вертикальный Резистор – горизонтальный Резистор – вертикальный ЭДС – горизонтальный (справа -, слева +) ЭДС – горизонтальный (справа +, слева -) ЭДС – вертикальный (вверху -, внизу +) ЭДС – вертикальный (вверху +, внизу -) | |
Важно
Чтобы добавить элемент в электрическую цепь, необходимо ввести тип элемента (например, резистор), указать краткое наименование элемента (например, R1 – для того, чтобы легче ориентироваться), также укажите величину (например, для резистора R1 – это 4 Ом – но, нужно ввести безразмерно, т.е. ввести 4)
Метод расчета электрической цепи с применением контурных токов
Для расчета электрической цепи методом контурных токов выбирается система независимых контуров, по которым протекают контурные токи, направление которых выбирается произвольно. Если ветвь включена только в одну цепь, ток в этой ветви равен току в цепи. Если ветвь включена в более чем одну цепь, ток в этой ветви равен сумме токов цепи, проходящих через эту ветвь, с учетом знака и выбранного направления. Контурные токи находят, решая систему уравнений, составленную по второму закону Кирхгофа для каждого контура. По найденным контурным токам определяют токи ветвей схемы.
Алгоритм расчета электрической цепи методом контурных токов
1. Вычерчиваем принципиальную схему цепи и обозначаем все элементы, задаем направления токов ветвей.
2. Определяем все независимые контуры.
3. Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры 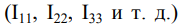
или римские цифры.
4. По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи уравнений учитывайте, что направление обхода цепи, из которого создаются уравнения, совпадает с направлением тока цепи в этой цепи. Необходимо учитывать тот факт, что в соседних ветвях, принадлежащих к двум цепям, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.
5. Решаем любым методом полученную систему относительно контурных токов и определяем их.
6. Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры 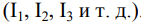
7. Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.
При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.
Возможно вам будут полезны данные страницы:
| Расчет электрической цепи методом эквивалентных преобразований |
| Расчет электрической цепи по закону Кирхгофа |
| Расчет электрической цепи методом наложения |
| Метод двух узлов |
Анализ электрических цепей методом контурных токов
Ток в любой ветви можно представить составленным из нескольких токов, каждый из которых замыкается по своему контуру, оставаясь вдоль него неизменным. Такие составляющие называются контурными токами.
Эти токи (токи ветвей связи) принимаются в качестве независимых переменных. т.е. при анализе рассматриваются главные контуры:
На основании закона Ома
Умножая левую и правую части уравнения на матрицу B, получим:
В то же время I(В)= BTI(K);
Обозначая ℤ(K)= Bℤ(В)BT – матрица контурных сопротивлений, E(K)= BE(В)− Bℤ(В)J(В) – матрица контурных ЭДС, получим уравнение контурных токов в матричной форме:
Развёрнутая форма контурных уравнений:
Направление обхода контуров совпадает с направлением контурных токов (токов ветвей связи).
Пример.
Ветви связи – 2 и 3, n = 2, m = 3.
Матрица контуров:
Матрица сопротивлений:
Матрица контурных сопротивлений:
Предыдущая