Векторная диаграмма токов и напряжений

Векторные диаграммы и комплексное представление

Векторные диаграммы можно считать вариантом (и иллюстрацией) представления колебаний в виде комплексных чисел. При таком сопоставлении ось Ox соответствует оси действительных чисел, а ось Oy – оси чисто мнимых чисел (положительный единичный вектор вдоль которой есть мнимая единица).

Тогда вектор длиной A, вращающийся в комплексной плоскости с постоянной угловой скоростью ω с начальным углом φ0 запишется как комплексное число

а его действительная часть

-есть гармоническое колебание с циклической частотой ω и начальной фазой φ0.

Хотя, как видно уже из вышесказанного, векторные диаграммы и комплексное представление колебаний теснейшим образом связаны и по сути представляют собой варианты или разные стороны одного и того же метода, они, тем не менее, обладают своими особенностями и могут применяться и по отдельности.

• Метод векторных диаграмм может излагаться отдельно в курсах электротехники или элементарной физики, если по тем или иным причинам (обычно связанным с умеренным уровнем математической подготовки учащихся и недостатком времени) надо избежать использования комплексных чисел (в явном виде) вообще.

• Метод комплексного представления (который при необходимости или желании может включать и графическое представление, что, правда, совершенно не обязательно и иногда излишне) вообще говоря более мощен, т.к. естественно включает в себя, например, составление и решение систем уравнений любой сложности, в то время как метод векторных диаграмм в чистом виде всё же ограничен задачами, подразумевающим суммирование, которое можно изобразить на одном чертеже.

• Однако метод векторных диаграмм (в чистом виде или в качестве графической составляющей метода комплексного представления) – более нагляден, а значит в некоторых случаях потенциально более надежен (позволяет до некоторой степени избежать грубых случайных ошибок, которые могут встречаться при абстрактных алгебраических вычислениях) и позволяет в некоторых случаях достичь в каком-то смысле более глубокого понимания задачи.

Разновидности векторных диаграмм

Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.

С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.

Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.

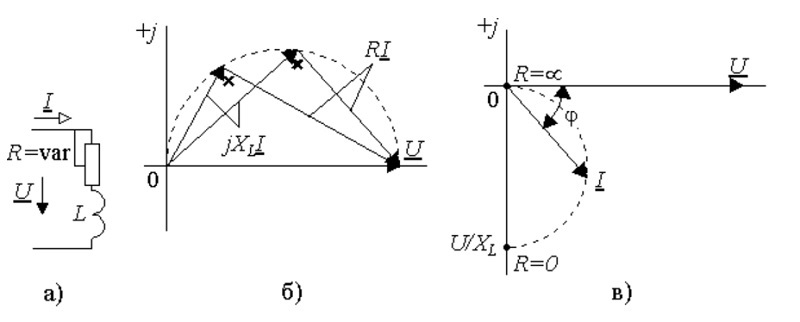
Круговая диаграмма

Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов. Индуктивный характер второй величины подразумевает перпендикулярное взаимное расположение, что хорошо видно на части рисунка б). Образованные треугольники отлично вписываются в сегмент окружности 180 градусов. Эта кривая соответствует всем возможным точкам, через которые проходит конец вектора UR при соответствующем изменении электрического сопротивления. Вторая диаграмма в) демонстрирует отставание тока по фазе на угол 90°.

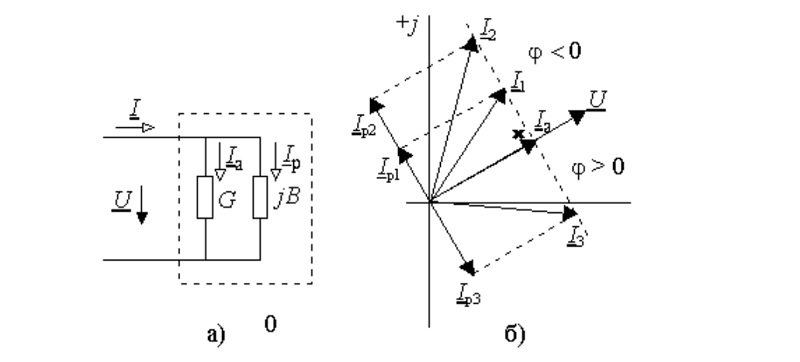
Линейная диаграмма

Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.

Механика; гармонический осциллятор

• Гармонический осциллятор в механике и гармонический осциллятор любой природы формально представляют точную аналогию, поэтому рассмотрим их в одном параграфе на примере механического гармонического осциллятора.
• Применение векторных диаграмм в механике сводится в основном к случаю гармонического осциллятора (в том числе имеется в виду и случай осциллятора с линейной по скорости силой трения); впрочем, векторные диаграммы могут быть до некоторой степени полезны и для исследования нескольких осцилляторов в том числе и в пределе бесконечного их количества (для колебаний или волн в распределенных системах).
• С современной точки зрения применение векторных диаграмм к гармоническому осциллятору представляет скорее только исторический и педагогический интерес, однако тем не менее в принципе они здесь вполне применимы.
• В механике применение векторных диаграмм (обычно подразумевается их применение к одномерному осциллятору) имеет ту особенность, что добавляющаяся вторая координата для превращения колебаний во вращение может иметь не только чисто формальный абстрактный смысл, но для одномерной механической системы такого сорта может быть указана механическая же двумерная система, для которой векторная диаграмма первой реализуется как вполне реальное двумерное механическое движение, и все векторы реально двумерны (а после проецирования всех их и движения точки двумерной системы на одну ось, мы получаем мгновенные значения соответствующих величин – в том числе положения – для соответствующей одномерной системы); таким образом, для механической одномерной системы возможна не только формальная математическая, но и реальная механическая модель, переводящая колебательное одномерное движение во вращательное движение в двумерном пространстве, реализующая в себе векторную диаграмму для одномерной системы.

Разберем два основных случая простого применения векторных диаграмм в механике (как замечено выше, также применимых к гармоническому осциллятору не только механической, но любой природы): осциллятор без затухания и без внешней силы и осциллятор с (линейным) затуханием (вязкостью), и внешней вынуждающей силой.

Векторная диаграмма – это удобный инструмент представления синусоидальных функций времени, коими являются, к примеру, напряжения и токи электрической цепи переменного тока.

Рассмотрим, например, произвольный ток, представленный в виде синусоидальной функции

i(t) = 10 sin(ωt + 30°).

Данный синусоидальный сигнал можно представить в виде комплексной величины

I = 10∠30°.

Для формирования комплексного числа используются модуль и фаза синусоидального сигнала.

Для построения векторных диаграмм сперва составляют уравнения по законам Кирхгофа для рассматриваемой электрической цепи.

Рассмотрим электрическую цепь, представленную на рис. 1, и нарисуем для неё векторную диаграмму напряжений. Обозначим падение напряжение на элементах.

Последовательное соединение элементов цепи

Составим уравнение для данной цепи по второму закону Кирхгофа:

UR + UL + UC = E.

По закону Ома падение напряжений на элементах определяется по следующим выражениям:

UR = I ∙ R,

UL = I ∙ jXL,

UC = −I ∙ jXC.

Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости. Обычно вектора токов и напряжений отображаются в своих масштабах: отдельно для напряжений и отдельно для токов.

Из курса математики известно, что j = 1∠90°, −j = 1∠−90°. Отсюда при построении векторной диаграммы умножение какого-либо вектора на мнимую единицу j приводит к повороту этого вектора на 90 градусов против часовой стрелки, а умножение на −j приводит к повороту этого вектора на 90 градусов по часовой стрелке.

При построении векторной диаграммы напряжений на комплексной плоскости сперва отобразим вектор тока I, после чего относительного него будем отображать вектора падений напряжений (рис. 2) с учётом приведённых выше соотношений для мнимой единицы.

Падение напряжения на резисторе UR совпадает по направлению с током I (т.к. UR = I ∙ R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Падение напряжения на индуктивном сопротивлении опережает вектор тока на 90° (т.к. UL = I ∙ jXL, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Падение напряжения на ёмкостном сопротивлении отстаёт от вектора тока на 90° (т.к. UC = −I ∙ jXC, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелке).

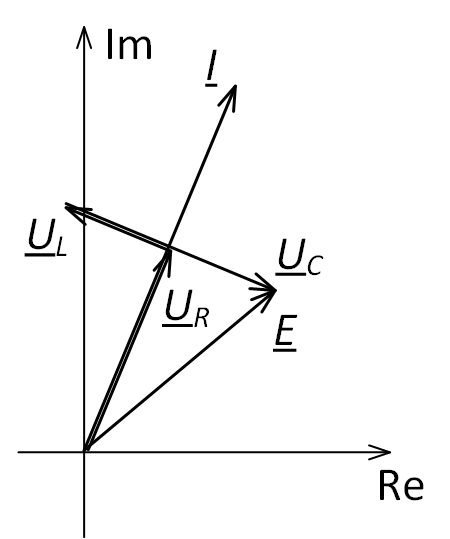
Векторная диаграмма напряжений при последовательном соединении элементов цепи

Следует обратить внимание, что на одной векторной диаграмме изображают только векторы тех величин, у которых частота совпадает!

Рассмотрим электрическую цепь, представленную на рис. 3, и нарисуем для неё векторную диаграмму токов. Обозначим направление токов в ветвях.

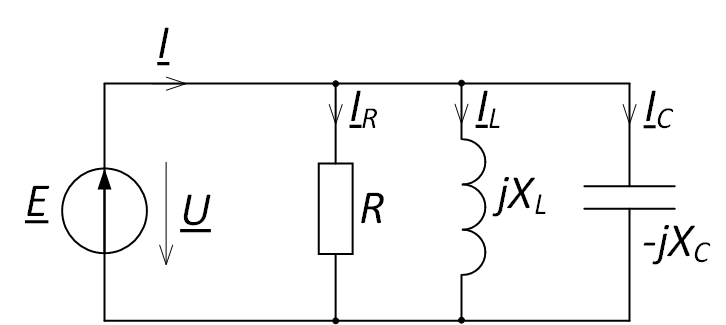
Параллельное соединение элементов цепи

Составим уравнение для данной цепи по первому закону Кирхгофа:

I­­ – IR – IL – IC = 0,

откуда

I­­ = IR + IL + IC.

Определим по закону Ома токи в ветвях по следующим выражениям, учитывая, что 1 / j = −j:

IR = E / R,

IL = E / (jXL) = −j ∙ E / XL,

IC = E / (−jXC) = j ∙ E / XC,

Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости.

При построении векторной диаграммы токов на комплексной плоскости сперва отобразим вектор ЭДС E, после чего относительного него будем отображать вектора токов токов (рис. 4) с учётом приведённых выше соотношений для мнимой единицы.

Ток в резисторе IR совпадает по направлению с ЭДС E (т.к. IR = E / R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Ток в индуктивном сопротивлении отстаёт от вектора ЭДС на 90° (т.к. IL = −j ∙ E / XL, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелки). Ток в ёмкостном сопротивлении опережает вектор ЭДС на 90° (т.к. IC = j ∙ E / XC, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Результирующий вектор тока определяется после геометрического сложения всех векторов по правилу параллелограмма.

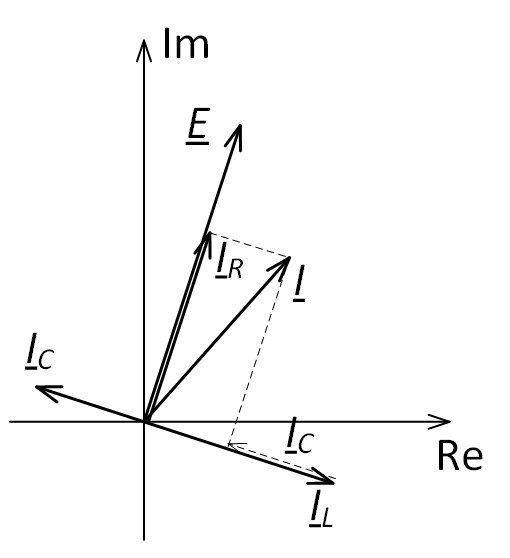
Векторная диаграмма токов при параллельном соединении элементов цепи

Для произвольной цепи алгоритм построения векторных диаграмм аналогичен вышеизложенному с учётом протекаемых в ветвях токов и прикладываемых напряжений.

Обращаем ваше внимание, что на сайте представлен инструмент для построения векторных диаграмм онлайн для трёхфазных цепей.

Как построить векторную диаграмму токов и напряжений

Расчеты в цепях с синусоидальными напряжениями и токами упрощаются, если вместо синусоид оперировать с их изображениями — вращающимися векторами (рис. 1).

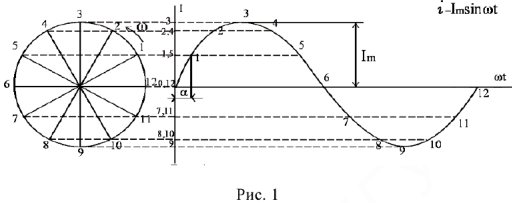
Проекция конца вектора на ось координат совершает синусоидальные колебания : каждое мгновенное значение тока, соответствующее моменту времени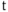
и фазовому углу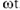
, можно рассматривать как проекцию на ось ординат вектора, повернувшегося на фазовый угол относительно оси абсцисс.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Таким образом, синусоидальная функция условно представляется вектором, длина которого определяется максимальным или действующим ее значением, а направление — ее начальной фазой; положительная начальная фаза откладывается от горизонтальной оси в сторону вращения векторов (против часовой стрелки). Векторы токов и напряжений, вращаясь с одной и той же

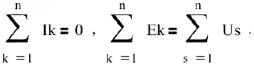
угловой скоростью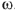
,. неподвижны относительно друг друга. Условное изображение синусоидально изменяющихся во времени токов и напряжении при помощи векторов позволило записать в векторной форме первый и второй законы Кирхгофа.

Алгебраическому суммированию синусоид, т.е. суммированию их мгновенных значений, соответствуют геометрические действия над изображающими их векторами. Применение в этой форме законов Кирхгофа даст возможность путем построения векторных диаграмм достаточно просто и наглядно рассчитывать электрические цепи. Приступая к графическому расчету пеней переменного тока, следует помнить, что физические процессы на участках цепи с сопротивлением, индуктивностью, емкостью весьма различны.

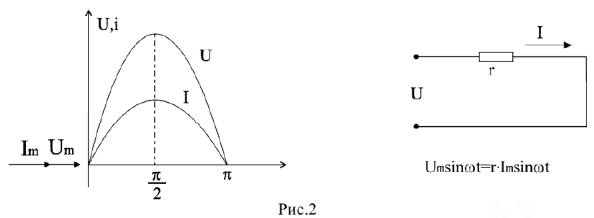
Соответственно вектор тока и вектор напряжения имеют одно направление.

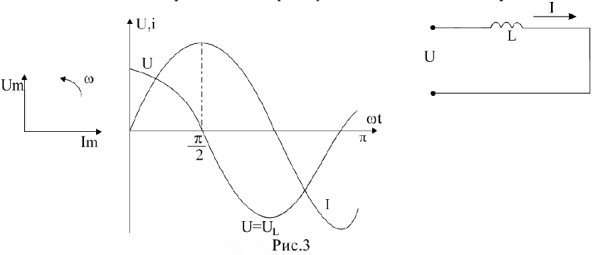
В индуктивном элементе ток отстает от напряжения на
и соответственно располагаются векторы (рис.3). Закон Ома для участка цепи только с индуктивными сопротивлением записывается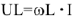
.

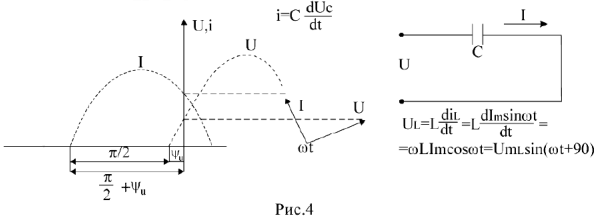
В емкостном элементе в активном сопротивлении ток и напряжение совпадают по фазе (рис.2), ток опережает напряжение на
( расположение вектора напряжения и тока показано на рис.4); закон Ома для участка цепи только с емкостным сопротивлением записывается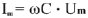
или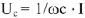

Рассмотрим расчет разветвленных электрических цепей с помощью векторных диаграмм.

Графоаналитический метод расчета

Графоаналитический метод расчета — это совокупность графического метода и метода пропорционального пересчета. Метод основан на том, что в линейной цепи токи пропорциональны напряжениям, векторная диаграмма напряжений и токов, рассчитанная и построенная для одного значения питающего цепь напряжения, сохранит свой вид при изменении величины этого напряжения, на диаграмме при этом изменятся лишь масштабы напряжений и токов.

Для цепи (рис.5) известны параметры

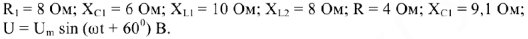
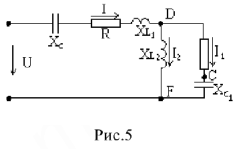
Требуется определить действующее значение токов ветвей, напряжений на участках цепи, начальные фазы токов и напряжений.

Построение векторной диаграммы начинается с наиболее удаленного источника элемента цепи, как говорят, с «конца» схемы. Принимаем масштабы для тока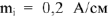
и для напряжения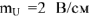
. Задаем значение тока в ветви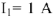
, определяем и строим на диаграмме напряжения на участках ветви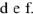
.

Падение напряжения на емкостном сопротивлении равно по величине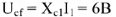
и отстает по фазе от тока
на 90° (вектор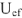
на диаграмме).

Падение напряжения на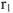
по величине равно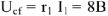
и совпадает по фазе с током
. Вектор напряжения ориентируем на диаграмме относительно тока
. Сумма векторов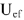
и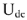
определяет напряжение на участке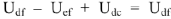
. Из диаграммы но масштабу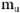
определяем величину напряжения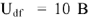
. Далее используем закон Ома для участка цепи с сопротивлением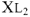
, находим ток
, так как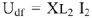
то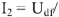

.

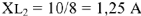
Для узла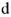
уравнение по первому закону Кирхгофа запишется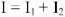
.

Определив величину тока
, построим вектор
, приняв за начало построения коней вектора тока
. Вектор тока
строится под углом
к вектору напряжения
— в сторону отставания, так как ток
— ток через индуктивный элемент, он оттает от напряжения на
. Сумма векторов токов
и
дает вектор
— ток в общей ветви цепи, он равен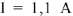
(взят в масштабе с диаграммы).

Запишем и графически решим уравнение по второму закону Кирхгофа для контура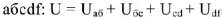
.

Перейдем к построению этого уравнения. Примем конец вектора
за начало построения вектора напряжения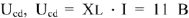
— падение напряжения на индуктивном сопротивлении. Вектор этого напряжения опережает по фазе ток
на
, строим его.

Принимаем конец вектора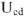
за начало построения вектора напряжения
на активном сопротивлении. Величина напряжения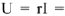

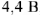
, вектор напряжения совпадает по фазе с током
, строим его параллельно вектору тока
. Принимаем конец вектора
за начало построения вектора
— напряжения на емкостном сопротивлении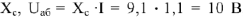
, вектор
отстает на
от вектора тока
.

Если теперь соединим начало координат (точку
с концом вектора
(точка «а» диаграммы напряжений), получим вектор приложенного к цепи напряжения
, равный 15В (с масштаба напряжений). Если напряжение, приложенное к цепи имеет другую величину, например, 90 В. то в силу линейности законов Кирхгофа все токи и падения напряжения увеличатся в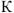
раз, где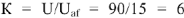
, но взаимное расположение вектором на диаграмме не изменится.

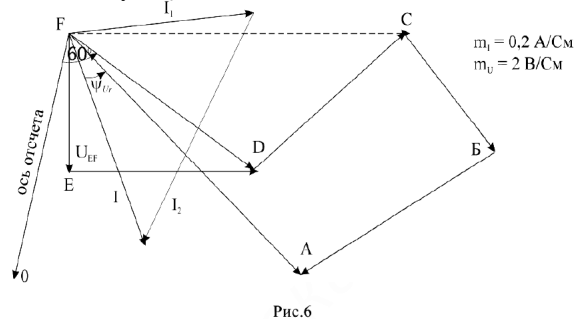
Входное напряжение имеет начальную фазу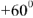
, учтем что и построим ось отсчета углов начальных фаз. К вектору напряжения
проведем луч
из начала построения (точка
под углом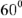
, луч
будет осью отсчета углов начальных фаз всех токов и напряжений.

Пользуясь векторной диаграммой, можно записать мгновенные значения всех рассчитанных величин. Например, ток во второй ветви:

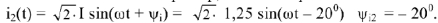
Напряжение участка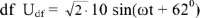
и т.д.

Построенная в такой последовательности векторная диаграмма напряжений носит название топографической.

Топографическая диаграмма

Топографические диаграммы представляют собой диаграммы комплексных потенциалов, причем каждой точке схемы соответствует определенная точка на топографической диаграмме.

Топографическая диаграмма позволяет измерить величину и начальную фазу напряжения любого участка цепи, не участвующею в расчете. Например,

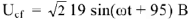
В действующее значение напряжения между точками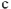
и
схемы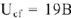
и начальная фаза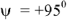
. тогда

Рассмотрим пример построения топографической диаграммы на комплексной плоскости.

Дана цепь (рис.7), её параметры:

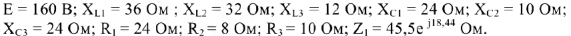
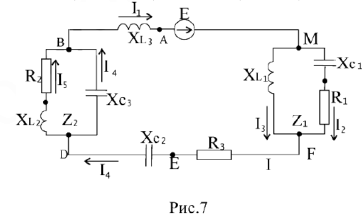
Комплексным методом рассчитаем токи цепи:

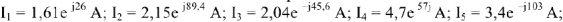
Строим на векторной плоскости диаграмму токов в масштабе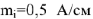
(рис.8). Для построения топографической диаграммы напряжений принимаем потенциал узла
равным нулю,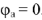
.

Тогда точка
будет находиться в начале координат комплексной плоскости. Вычислим комплексы напряжении на каждом из элементов цепи, обходя из точки
цепь против направления тока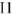
. При таком направлении обхода напряжение
на сопротивлении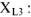

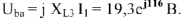
Строим вектор
на комплексной плоскости (рис.8).

Из точки
под углом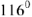
к действительной полуоси +1 откладываем модуль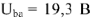
в масштабе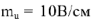
. Вершина построенного вектора соответствует точке
. Стрелку вектора
следует направить к точке
т.е противоположно направлению стрелки напряжения
на схеме цепи, топографической диаграмме вектор
должен опережать но фазе вектор тока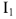
на 90°. Находим напряжение на сопротивлении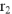
:

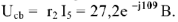
По полученному выражению из точки
строим вектор
Вершиной вектора
является точка
.

Контроль построения: вектор
должен совпадать по фазе с вектором тока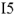
.Теперь находим напряжение на индуктивности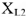
:

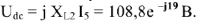
Из точки
строим вектор
. Вершиной построенного вектора является точка
.

Контроль построения: вектор
должен опережать по фазе вектор тока
на
. Переходя по контуру в выбранном направлении, находим последовательно положение точек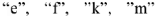
на комплексной плоскости. Вектор, соединяющий начало координат и точку
. представляет собой ЭДС источника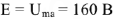
.

Пользуясь топографической диаграммой, легко определить напряжения между любыми точками цепи. Например, комплекс напряжения
определяется вектором, соединяющим точки
и
и направленным к точке
(показан на рис.8 пунктиром). Измеряя на диаграмме модуль и начальную фазу вектора
находим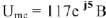
.

ПримсрЗ. Рассмотрим расчет цепи на рис.7 графоаналитическим методом

Зададимся условным значением тока

, пусть
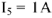
. В масштабе

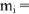
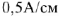
строим значение тока
, полагая, что точка
находится в начале координат. Выбранному условному значению тока
однозначно соответствуют условные значения всех остальных токов и напряжений в цепи. Эти напряжения и токи снабжаем меткой «штрих». Находим напряжение

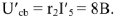
В масштабе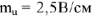
строим вектор напряжения
, совпадающий по фазе с вектором тока
( рис.9).

Вычислив напряжение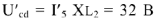
, строим вектор напряжения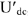
, опережающий по фазе вектор тока
на 90′. Соединив точки
и
, получаем вектор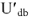
. Измеряя линейкой его длину с учетом масштаба напряжений, находим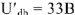
. По закону Ома находим ток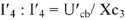

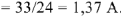
Из конца вектора тока
строим вектор тока
, опережающий по фазе вектор напряжения
на
. Векторно суммируя токи
и
находим ток
. Измеряя линейкой длину вектора тока
находим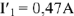
. Зная токи
вычисляем напряжения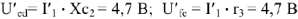
.

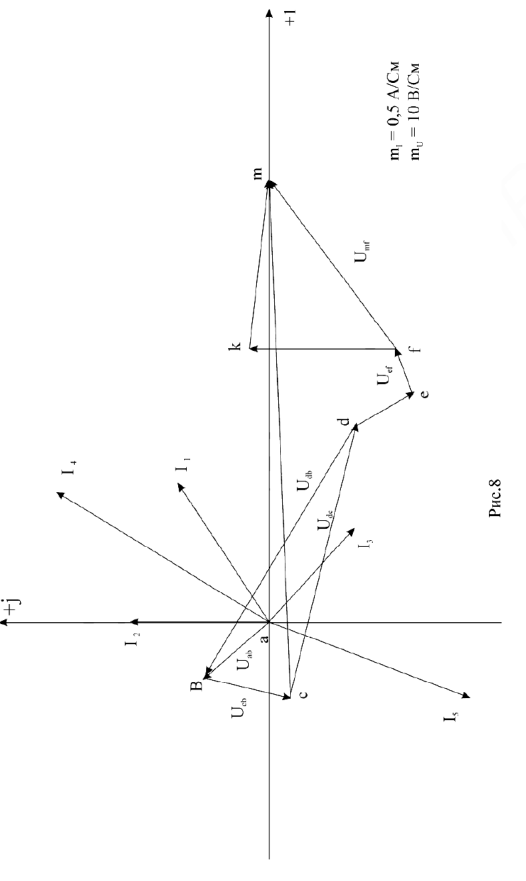
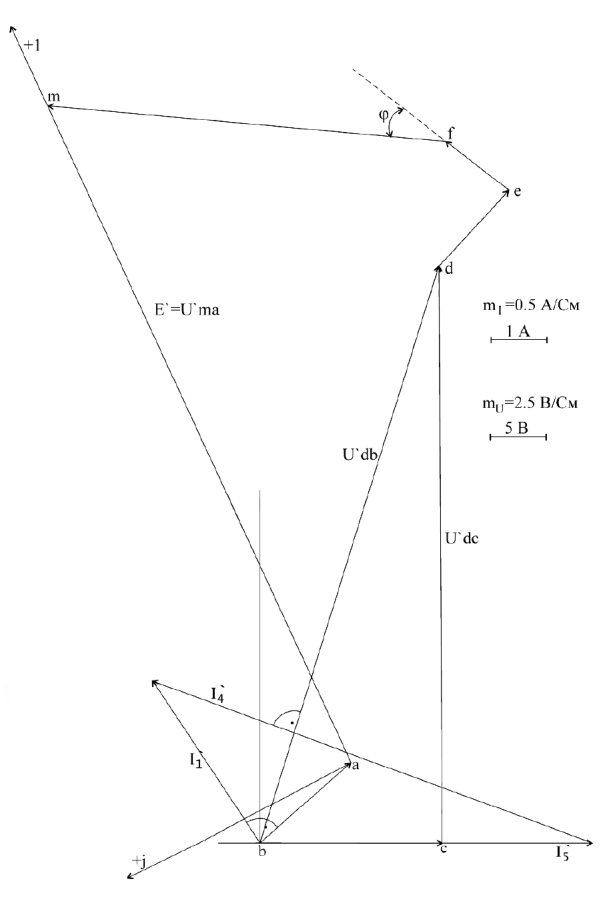
Рис.9

Из точки
строим вектор напряжения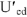
, отстающего но фазе от тока
на
и вектор напряжения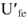
совпадающего по фазе с током
. Чтобы определить токи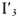
и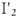
для участка
цепи, построим дополнительную векторную диаграмму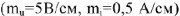
. Пусть

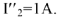
Тогда

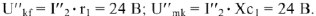
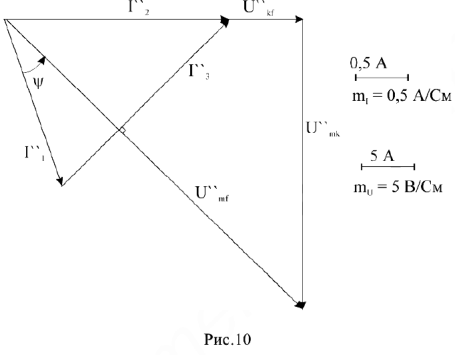
С учетом фазовых соотношений между током
и напряжениями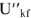
строим диаграмму (рис. 10). Измеряя длину вектора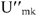
, с учетом масштаба напряжений находим его величину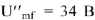
. Тогда величина тока
определяется следующим образом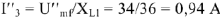
.

Построив вектор
и суммируя векторы токов
и
, из диаграммы на рис. 10 находим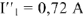
.

Чтобы привести диаграмму на рис.10 в соответствие с найденными ранее значениями тока
, находим коэффициент пересчета

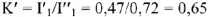
Умножая длины всех векторов на рис.10 на коэффициент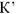
и сохраняя неизменными фазовые углы, получим векторную диаграмму участка
, соответствующую току
.

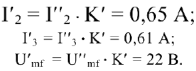
Измеряем угол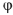
на диаграмме рис.10:

Под углом
по отношению к вектору
на рис.9 из точки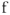
строим вектор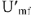
. Найдем теперь напряжение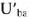
:

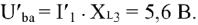
Поскольку напряжение
, опережает по фазе ток
на 90°. то вектор
строится так, как показано на Рис.9. Соединяя точки
и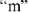
получаем вектор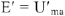
. Измеряя его длину находим

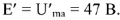
Векторная диаграмма на рис.9 является также и топографической диаграммой. ЭДС
превышает ЭДС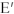
в
раз:

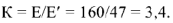
Поскольку рассчитываемая цепь линейна, то напряжения и токи, вызываемые ЭДС
, превышают условные напряжения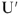
и токи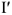
также в
= 3.4 раза.

Таким образом

Чтобы измерить начальные фазы токов и напряжений, следует на рис.9 выбрать такую систему координат, в которой ЭДС
имеет соответствующую заданию начальную фазу. Так как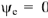
, то поместив начало координат в точку
, действительную полуось совмещаем с направлением ЭДС
, а полуось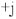
строим ортогонально оси 4 1, как показано на рис.9.

Рассмотрим пример построения векторной диаграммы по известным токам и напряжениям (действующие значения напряжений и токов получены экспериментально). В этом случае при помощи векторной диаграммы можно решить обратную задачу расчета цепи: но токам и напряжениям цепи определить эквивалентные параметры двухполюсников, составляющих цепь.

Разновидности векторных диаграмм и правила их построения

Определение 1

Векторная диаграмма – это совокупность векторов на комплексной прямой, которая соответствует комплексным параметрами и/или величинам электрической цепи.

Векторные диаграммы могут быть:

1. Точеными.
2. Качественными.

Построение точечных диаграмм осуществляется с соблюдением масштаба всех величин согласно результатам численного анализа. Основное назначение точечных диаграмм – проверка результатов расчета. Качественные векторные диаграммы строятся с учетом взаимосвязей между комплексными величинами. Построение данного вида диаграмм, как правило, заменяет расчет, или предшествует ему. В качественных векторных диаграммах значения параметров (или величин) и масштаб изображения несущественны. Основное требование к ним заключается в том, чтобы все связи между величинами были отображены корректно. Этот вид диаграмм является одним из основных инструментов анализа цепей переменного тока.

Векторные диаграммы делятся на круговые и линейные. В круговой векторной диаграмме геометрическим местом точек перемещения конца вектора является окружность или полуокружность. В линейных векторных диаграммах геометрическим местом точек конца вектора является прямая линия.

Перед построением векторной диаграммы сначала вычерчивается и анализируется схема замещения, которая эквивалентна принципиальной схеме электрической цепи. На данной схеме обязательно отмечаются каждый элемент электрической цепи, наносятся направления всех напряжений и токов. Векторные диаграммы токов и напряжений должны чертиться в крупных масштабах, выбор которого осуществляется по самой большой вычисленной или измеренной величине электрического тока или напряжения.

Построение ВД напряжений и токов

В качестве примера построения ВД рассмотрим последовательную цепочку из сопротивления R, индуктивности L и конденсатора C. Схема приведена на рисунке ниже.

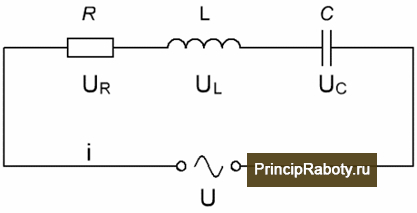
Напряжения на элементах схемы — UR, UL, UC. Ток в цепи — i.

Напряжение на выходе U = UR + UL + UC.

Пускай в цепи протекает синусоидальный ток с частотой ω и с нулевым сдвигом фазы. Для ненулевого сдвига фазы ВД просто повернётся на этот начальный угол, а общий её вид не изменится. Амплитуды напряжений на каждом элементе в форме закона Ома:

|U|R = R* |i|

|U|L = 1/ωC*|i|

|U|С = ωL* |i|

Соответствующие этим амплитудам длины векторов наносятся на ВД. При этом каждый вектор наносится с учетом своего фазового сдвига. Суммарный вектор оказался равен U = UR + UL + UC, но это теперь доказано геометрически на диаграмме.

Модуль суммарного вектора равен длине гипотенузы в прямоугольном треугольнике со сторонами |U|R, (|U|L – |U|С). Воспользовавшись теоремой Пифагора, можно вычислить |U|:

|U|2 = UR2 + (UL – UC)2

Применив формулы, указанные выше, получим:

|U|2 = (i0 * R)2 + (i0 * ωL – i0/ ωC)2

Можно вынести за скобки i0 (амплитуда тока — длина вектора i), тогда:

|U|2 = i02 * (R2 + (ωL – 1/ ωC)2

Пользуясь последней формулой, можно вычислять амплитуду синусоидального напряжения. Полученные формулы справедливы для случая обратной задачи, когда требуется найти ток в цепи с известным источником напряжения.

Предыдущая

РазноеЭлектротехника для чайников. Как научиться разбираться в электрике: уроки для начинающих

Следующая

РазноеАвтоматический выключатель — от чего защищает и как он устроен