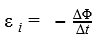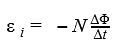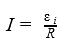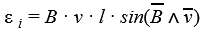Магнитная индукция. Определение и описание явления

Теория

Электромагнитное поле – аналог механической силы, проявляется воздействием на перемещающиеся носители электрического заряда, тела с магнитным моментом. Характеризуется механической силой, которое поле оказывает на проводники либо магниты.

Опыты показывают, что магнитное поле пытается сориентировать магнитную стрелку, развернуть её относительно плоскости витка, в направлении, которое называется направлением поля. Для планеты его принимают за линию, направленную с географического севера на юг. Электрическое поле характеризуется векторной величиной E – напряженностью. Для описания магнитного воздействия применяют величину B, названную магнитной индукцией.

Во избежание путаницы характеристики носят разные названия.

Направлением B считают то, куда укажет магнитная стрелка относительно витка с электрическим током. Его модуль определяют по максимальному значению вращающего момента Mmax, действующего на стрелку. При одинаковом значении индукции в каждой точке пространства поле называется однородным, когда его величина проявляется в веществе в разной степени – неоднородным.

Магнитное поле: все формулы

В однородное поле помещают плоские контуры – изготовленные из точнейшей проволоки замкнутые проводники – с током. Измерения пикового вращающего момента показывает, что он:

1. прямо пропорционален силе протекающего через контур электрического тока I;
2. зависит от площади контура S;
3. не зависит от формы замкнутого проводника при равной площади.

Магнитный момент контура с током равен:

pm = IS.

Рассмотрим остальные формулы, позволяющие рассчитать электромагнитное поле.

Вращающий и магнитный моменты характеризуют электромагнитную индукцию, по модулю она равняется:

B= Mmax : pm.

Измеряется в теслах (Тл), названа в честь величайшего сербского учёного XX века Николы Теслы.

При расчётах неоднородных полей в них помещают маленькие контуры, по габаритам сравнимые с расстояниями, на которых наблюдаются изменения.

Магнитное полевое образование характеризуется напряжённостью H, пропорциональной индукции в вакууме:

B = μ0H,

μ0 = 4π*10-7 Гн/м или Тл*м/А.

При вычислениях для вещества добавляется коэффициент магнитной проницаемости μ, для вакуума он равен единице.

B = μ μ0H.

Магнитная индукция соленоида:

B = μ0nI, здесь:

• n = N : l, N – число витков катушки, l – её длина;
• I – сила протекающего тока.

Формула энергии W магнитного поля для соленоида:

W = LI2 : 2 = ФI : 2

• L – индуктивность катушки;
• I – сила тока;
• Ф – магнитный поток.

Сила взаимодействия между проводниками с электрическим током:

F = μ μ0I1I2l : 2πr, здесь:

• I1, I2 – сила тока в обоих проводниках;
• l – их длина;
• r – расстояние между проводами с током.

Наибольший момент:

Mmax= BIS;

S – площадь контура.

Электромагнитное поле образуется вокруг намагниченных тел и проводников с током.

Поделитесь в социальных сетях: 18 октября 2021, 18:15 Физика 0.00% 00

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Опыты Фарадея

• На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
• Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
• Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• источник – переменное магнитное поле;
• обнаруживается по действию на заряд;
• не является потенциальным;
• линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Физический смысл магнитной индукции

Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.

В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.

При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.

Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.

Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.

Формула магнитной индукции

где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.

Другие формулы, где встречается B

Эти формулы также можно использовать для её расчёта.

Сила Ампера:

Сила Ампера: Fa=IBL sinα

Где:

• Fa — сила Ампера (в Н — ньютон)
• I — сила тока (в А — ампер)
• B — индукция магнитного поля (в Тл)
• L — длина проводника (в м)
• α — угол между вектором В и одним из направлений (силы тока, скорости или др.; измеряется в рад. или град.)

Сила Лоренца:

Сила Лоренца: Fл = qvB sinα

Где:

• Fл — сила Лоренца (в Н — ньютон)
• q — заряд частицы (в Кл — кулон)
• v — скорость (в м/с)
• B — индукция (в Тл)
• α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))

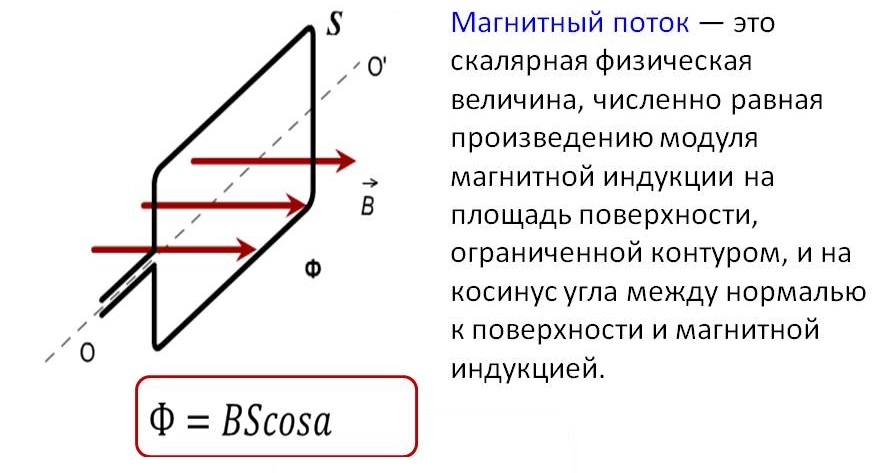
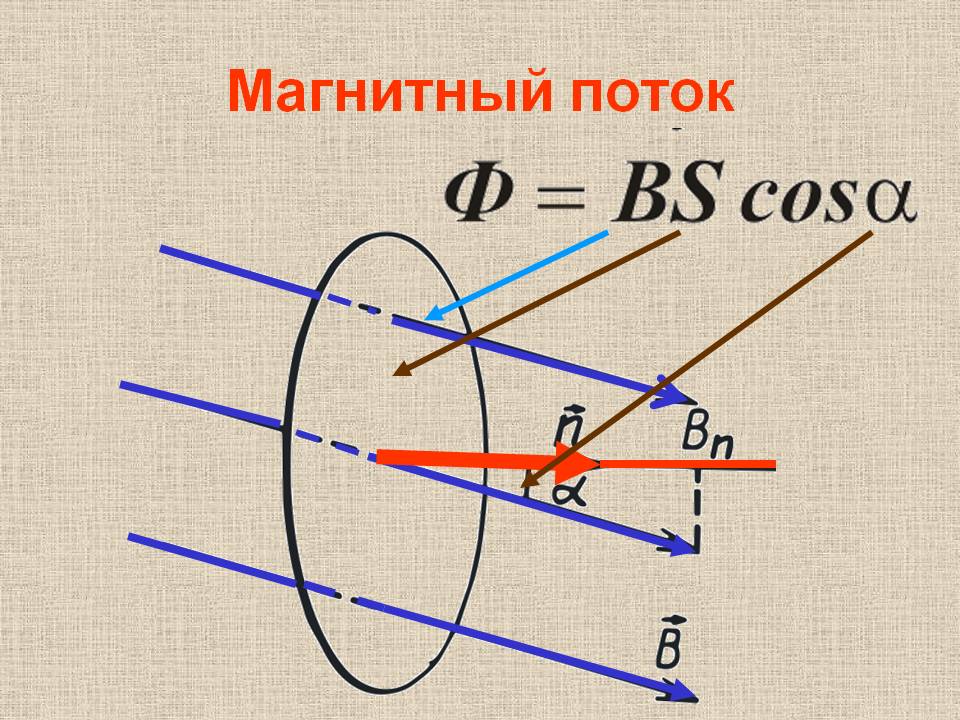
Магнитный поток:

Магнитный поток: Ф = BS cosα

Где:

• Ф — магнитный поток (в Вб – вебер)
• B — индукция (в Тл)
• S — площадь рамки (в м²)
• α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))

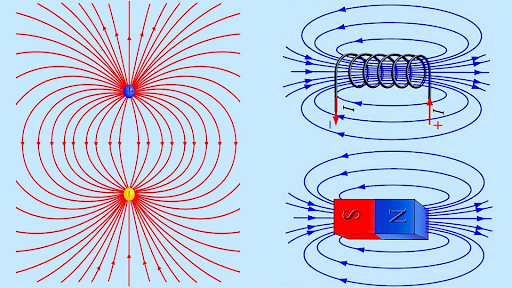
Направление линий магнитной индукции

Рассматриваемая индукция является векторной величиной, то, куда она направлена, определяется посредством помещаемой в поле магнитной стрелки: местоположение северного полюса будет направлением вектора. Поместив стрелку вблизи катушки или в какую-либо иную точку поля, можно определить, куда направлен вектор в этой конкретной точке.

Важно! Можно воспользоваться также правилом буравчика: когда он движется в одну сторону с током, вектор идет в одну сторону с вращением ручки.

Направление вектора МИ

Направление магнитных полей может указать стрелка магнита, помещаемая в эти поля. Она будет крутиться до тех пор, пока не остановится. Северный конец стрелки покажет, куда ориентирован B→ орт того или иного поля.

Линии магнитной индукции

Таким же образом ведёт себя рамка с током, имеющая возможность без помех ориентироваться в МП. Направленность вектора индукции указывает ориентацию нормали к такому замкнутому электромагнитному контуру.

Внимание! Здесь используют правило буравчика (правого винта). Если винт вращать так, как направлен ток в рамке, то поступательное продвижение винта совпадёт с направлением положительной нормали.

В некоторых случаях, чтобы найти направление, применяют правило правой руки.

Наглядное отображение линий МИ

Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.

Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.

С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.

Основные формулы для вычисления вектора МИ

Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.

Закон электромагнитной индукции

Закон электромагнитной индукции (закон Фарадея) звучит так:

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.

Математически его можно описать формулой:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​R​:

Если проводник длиной l будет двигаться со скоростью ​v​ в постоянном однородном магнитном поле с индукцией ​B​ ЭДС электромагнитной индукции равна:

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
• вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Закон Био-Савара-Лапласа

Формула индукции ЭДС

Описывает правила поиска B → магнитного поля, которое создает постоянный электрический ток. Это экспериментально установленная модель. Био и Савар в 1820 году показали это на практике, Лаплас смог его сформулировать. Этот закон является фундаментальным в магнитостатике. На практике рассматривался фиксированный провод малого сечения, по которому пропускался электрический ток. Для исследования был выбран небольшой участок проволоки, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.

Интересно. Лаплас Пьер Симон предложил также рассматривать движение электрона как ток и на этом утверждении с помощью этого закона доказал возможность определения МП наступающего точечного заряда.

Согласно этому физическому правилу каждый сегмент dl проводника, по которому протекает электрический ток I, образует магнитное поле dB в пространстве вокруг себя с интервалом r и под углом α:

дБ = µ0 * I * dl * sin α / 4 * π * r2,

где это находится:

• дБ – магнитная индукция, Тл;
• µ0 = 4 π * 10-7 – магнитная постоянная, Гн / м;
• I – сила тока, А;
• dl – отрезок жилы, м;
• r – расстояние от точки, где находится магнитная индукция, м;
• α – угол, образованный r и вектором dl.

Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП требуемого тока. Он будет равен векторной сумме.

Закон Био-Савара-Лапласа

Существуют формулы, описывающие этот закон для отдельных случаев МП:

• поля прямого движения электронов;
• поля кругового движения заряженных частиц.

Формула депутата первого рода:

В = µ * µ0 * 2 * I / 4 * π * r.

Для кругового движения это выглядит так:

В = µ * µ0 * I / 4 * π * r.

В этих формулах µ – (относительная) магнитная проницаемость среды).

Рассматриваемый закон следует из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, когда электрическое поле постоянно, только что рассматривали Био и Савар.

Принцип суперпозиции

Для МП существует принцип, согласно которому полный вектор магнитной индукции в определенной точке равен векторной сумме всех векторов MI, созданных разными токами в данной точке:

B → = B1 → + B2 → + B3 →… + Bn→

Правило Ленца

Для определения направления индукционного тока необходимо использовать правило Ленца.

С академической точки зрения это правило звучит так: индукционный ток, возбуждаемый в замкнутой цепи при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле предотвращает изменение магнитного потока, вызывая индукционный ток.

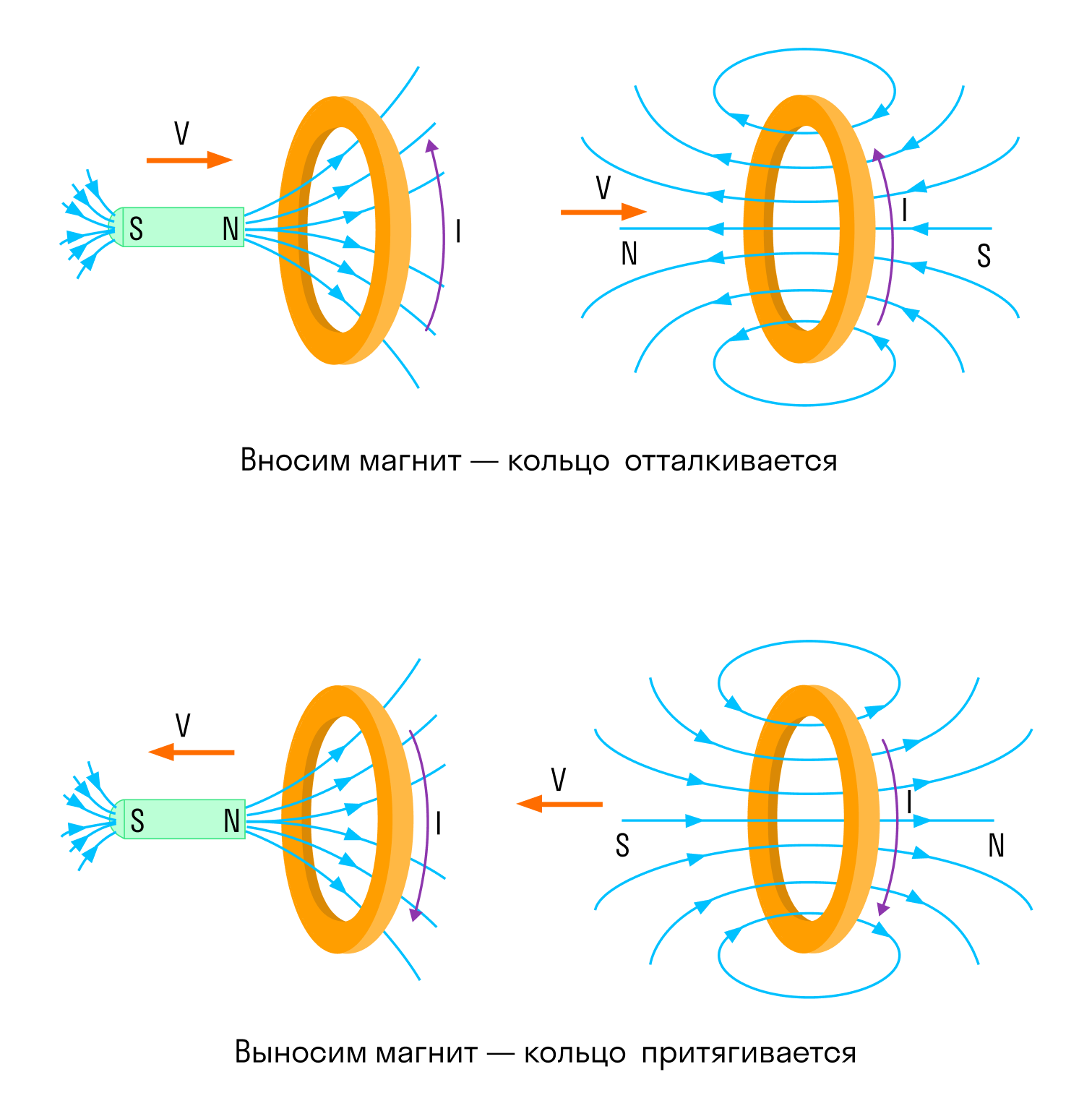
Попробуем немного попроще: катушка в данном случае – недовольная бабушка. Они забирают магнитный поток: она несчастна и создает магнитное поле, которое этот магнитный поток хочет восстановить.

Они дают ей магнитный поток, они принимают его, они говорят, они используют его, и она такая – “Потому что ваш магнитный поток сдался мне!” и создает магнитное поле, которое вытесняет этот магнитный поток.

Что такое катушка индуктивности

Что вы себе представляете под словом «катушка» ? Ну… это, наверное, какая-нибудь «фиговинка», на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.

Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!

Типы катушек индуктивности

Катушки индуктивности делятся в основном на два класса: с магнитным и  немагнитным сердечником. Снизу  на фото катушка с немагнитным сердечником.

Но где у нее сердечник? Воздух — это немагнитный сердечник :-).  Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным  сердечником используется, когда индуктивность не превышает 5 миллигенри.

А вот катушки индуктивности с сердечником:

В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.

Для катушек средней индуктивности используются ферритовые сердечники:

Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.

Что влияет на индуктивность?

От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов.  Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC — метр мне показывает ноль.

Имеется ферритовый сердечник

Начинаю вводить катушку в сердечник на самый край

LC-метр  показывает 21 микрогенри.

Ввожу катушку на середину феррита

35 микрогенри. Уже лучше.

Продолжаю вводить катушку на правый край феррита

20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине.  Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности  в переменных катушках индуктивности:

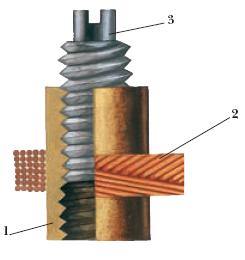
где

1 — это каркас катушки

2 — это витки катушки

3 — сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.

Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки

Индуктивность стала почти 50 микрогенри!

А давайте-ка попробуем расправим витки по всему ферриту

13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо «виток к витку».

Убавим витки катушки в два раза. Было 24 витка, стало 12.

Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз.  Вывод: чем меньше количество витков — тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.

[quads id=1]

Давайте поэкспериментируем с ферритовым кольцом.

Замеряем индуктивность

15 микрогенри

Отдалим витки катушки друг от друга

Замеряем снова

Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка  не играет никакой роли в катушке индуктивности тороидального исполнения.

Мотнем побольше витков. Было 3 витка, стало 9.

Замеряем

Офигеть! Увеличил количество витков  в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.

Если верить формулам для расчета индуктивностей, индуктивность зависит от «витков в квадрате». Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.

Последовательное и параллельное соединение катушек индуктивности

При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.

А при параллельном соединении получаем вот так:

При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек.  Это может привести к неправильным показаниям общей индуктивности.