Что такое энергия магнитного поля
Энергия магнитного поля — величина, обозначающая работу, затраченную электрическим током в проводнике или катушке индуктивности на образование этого магнитного поля.
Существует зависимость энергии магнитного поля от индуктивности проводника, вокруг которого это поле образовалось. Для обозначения величины используют букву W. Единицами измерения энергии являются Дж/м3 или МГсЭ (Мега Гаусс Эрстеды). К примеру, максимальное значение энергии магнитного поля неодимовых магнитов равно 278-360 Дж/м3, а ферритовых — составляет до 30 Дж/м3.
Описание явления, закон Фарадея
Магнитное поле обладает энергией. Данный факт можно доказать с помощью практического эксперимента. Опыт заключается в исследовании процесса убывания силы тока в катушке при отключении от нее источника тока. Предположим, что до того момента, когда был разомкнут ключ, в катушке имелся ток I, что способствовало образованию магнитного поля. После размыкания ключа катушка и сопротивление соединяются последовательно. В результате самоиндукции ток в катушке будет постепенно уменьшаться. Процесс сопровождается выделением теплоты на сопротивлении. Источник тока отключен, поэтому необходимо определить источник энергии, которая расходуется на тепло. Так как убывает ток и создаваемое им магнитное поле, допустимо говорить о понятии энергии тока или энергии магнитного поля, которое он создает.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В том случае, когда магнитное поле образовано постоянным током, определить место сосредоточения энергии не представляется возможным, так как ток по своему свойству образует магнитное поле, которое в любом случае сопровождается токами. Можно рассмотреть переменное магнитное поле в электромагнитной волне. Такая волна характеризуется наличием магнитных полей в условиях отсутствия токов. Известно, что электромагнитные волны являются переносчиками энергии, что позволяет сделать вывод о существовании энергии в магнитном поле. Таким образом, электрический ток обладает энергией, локализованной в магнитном поле, то есть в среде, окружающей этот ток. Согласно закона сохранения энергии, на примере эксперимента вся энергия магнитного поля выделяется в виде Джоулева тепла на сопротивлении R.
Определение
Электромагнитная индукция представляет собой явление возникновения электрического тока, поля или электрической поляризации при изменении с течением времени магнитного поля или в процессе движения материальной среды в нем.
С помощью опытов с катушками и магнитом Фарадею удалось обнаружить зависимость между величиной электродвижущей силы и скорости, с которой перемещаются катушки или магнит. Данное наблюдение послужило основанием для выявления закономерности и формулировки закона электромагнитной индукции.
Определение
Закон электромагнитной индукции: электродвижущая сила пропорциональна скорости изменения магнитного потока, проходящего через контур.
Единицами измерения ЭДС являются вольты магнитного потока — веберы. Формула закона Фарадея содержит знак минуса. К данному выражению применено правило Ленца, как пояснение того, что ток, образовавшийся в результате индукции, в любом случае противоположно направлен образующему его магнитному потоку. Магнитное поле индукционного тока всегда препятствует магнитному потоку из внешнего источника. По смыслу правило схоже с законом сохранения энергии.
Потоки энергии электромагнитного поля
Для электромагнитной волны плотность потока энергии определяется вектором Пойнтинга S (в русской научной традиции — вектор Умова — Пойнтинга).
В системе СИ вектор Пойнтинга равен векторному произведению напряжённостей электрического и магнитного полей и направлен перпендикулярно векторам E и H. Это естественным образом согласуется со свойством поперечности электромагнитных волн.
Вместе с тем, формула для плотности потока энергии может быть обобщена для случая стационарных электрических и магнитных полей и имеет тот же вид. Факт существования потоков энергии в постоянных электрических и магнитных полях может выглядеть странно, но не приводит к каким-либо парадоксам; более того, такие потоки обнаруживаются в эксперименте.
Индуктивность в системе магнитно-связанных катушек
Рассмотрим частный случай, когда две магнитно-связанные катушки электрически соединены между собой последовательно, в результате чего в обеих катушках ток I один и тот же. Энергия магнитного поля такой системы
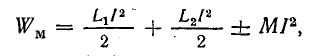
или
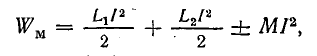
где 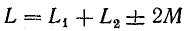
— индуктивность системы магнитно-связанных катушек.
При согласном включении
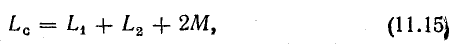
при встречном включении
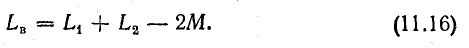
Выражение энергии через характеристики магнитного поля
Формулами (11.13) и (11.14) энергия выражена через характеристики контуров с токами.
Можно показать, что в данном случае энергия распределена в магнитном поле, окружающем проводники с токами.
Для примера возьмем поле катушки с кольцевым сердечником. Если диаметр сечения сердечника много меньше диаметра самого сердечника, поле можно считать равномерным:
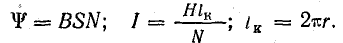
Тогда
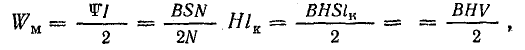
где 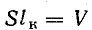
— объем сердечника.
Энергия магнитного поля в единице объема

Здесь энергия выражена через характеристики магнитного поля, что свидетельствует о ее принадлежности магнитному полю.
Задача 11.8.
Определить энергию магнитного поля в системе двух обмоток (задача 8.21) при согласном и встречном их включении, если ток в первой обмотке I1 = 5 А, а во второй I2 = З А.
Решение. Для определения энергии в магнитно-связанной системе двух обмоток воспользуемся формулой (11.14).
Величины индуктивностей катушек и взаимной индуктивности при неферромагнитном сердечнике не зависят от тока в них, поэтому возьмем их по результатам решения задачи 8.21:
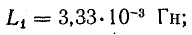
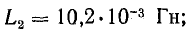
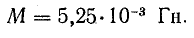
При согласном включении обмоток
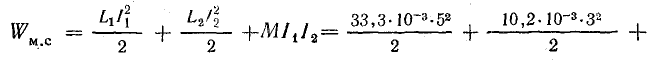
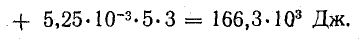
При встречном включении
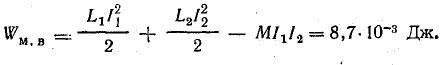
Задача 11.9.
Общая индуктивность двух последовательно соединенных катушек (см. рис. 8.22) при согласном включении равна 1,52 мГн, при встречном — 0,88 мГн. Определить взаимную индуктивность катушек.
Решение. Найдем взаимоиндуктивность катушек, решив совместно уравнения (11.15) и (11.16):
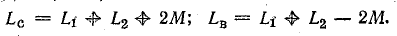
Вычтем второе уравнение из первого:
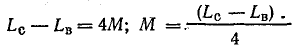
.
В данном случае 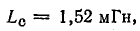
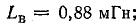
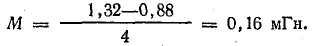
От чего зависит величина
Существует ряд некоторых ограничений в применении формулы для расчета энергии магнитного поля. При записи выражения выполнялось несколько условий:
- индуктивность контура, а также магнитная проницаемость вещества стабильны;
- вся энергия источника тока трансформируется в энергию магнитного поля.
Перечисленные условия справедливы лишь в случае вакуума, то есть при (mu)=1. Если контур с током поместить в вещество, то необходимо принимать во внимание следующие параметры:
- намагничивание вещества, что способствует его нагреву;
- объем и плотность вещества в магнитном поле могут изменяться даже при стабильной температуре.
Таким образом, магнитная проницаемость вещества (mu), изменяющаяся при перепадах температуры и плотности среды, не может оставаться постоянной в процессе намагничивания. Также работа источника ЭДС не полностью трансформируется в энергию магнитного поля. В том случае, когда объем вещества изменяется в малой степени, сохраняется стабильной температура среды, внешняя работа затрачивается на увеличение энергии магнитного поля и на теплоотдачу Q, чтобы поддерживать постоянную температуру.
Работа внешних сил, в нашем случае источника тока, совершаемая над телом при квазистатическом изотермическом процессе, соответствует увеличению свободной энергии тела. Таким образом, формула определяет часть свободной энергии намагниченного вещества, которая обладает связью с магнитным полем:
Выражение применимо при рассмотрении ситуаций в условиях вакуума для парамагнетиков и диамагнетиков. Но при опытах с ферромагнетиками магнитная индукция и напряженность магнитного поля связаны нелинейно, даже при T=const.
Энергия электромагнитного поля: формула, обозначение, в чём измеряется
При проведении опытов с катушкой и лампочкой накаливания в электрической цепи можно заметить интересное явление. После отключения индукции от источника электропитания, подключенная к ней параллельно лампа накаливания даёт кратковременную вспышку. В сети возникает ток благодаря воздействию электродвижущей силы самоиндукции. В качестве источника энергии для явления задействуется магнитное поле соленоида.
Для простоты расчёта предположим, что сила тока в цепи снижается линейно.
ЭДС самоиндукции при этом вычисляется по формуле:
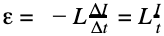
где t – время, за которое ток падает до нуля.
За этот временной интервал в цепи «пробегает» заряд:
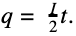
Проделанная магнитным полем работа равняется:
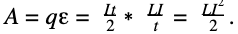
Это максимальная энергия магнитного поля катушки, вычисляется по формуле (обозначается Wm или W):
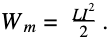
Читается как: сила магнитного поля катушки равняется половине произведения квадрата силы протекающего по ней тока I на индуктивность L.
Для конденсатора вычисляется иначе: 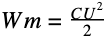
, C-ёмкость конденсатора.
Многие не знают, в чем измеряется энергия магнитного поля тока катушки. В системе единиц СИ это джоуль (Дж), названный в честь британского физика.
Графический вывод формулы
Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:
В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:
Wм=ΦI2=LI22=Φ22L
Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:
Wм=μ0·μ·n2·I22V=B22μ0·μV
В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.
Определение 4
Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.
В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.
Задача
Определить силу тока в соленоиде с индуктивностью 20 мГн, необходимую для генерирования энергии магнитного поля, равной 5 Дж.
Воспользуемся известной формулой: 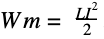
, отсюда 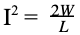
.
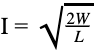
. Подставим значения, зная, что 20 мГн = 0,02 Гн.
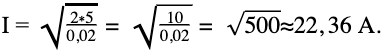
Ответ: 22,36 А.
Ограничения в применении формулы для вычисления плотности энергии магнитного поля
При получении формулы (9) считалось, что:
- индуктивность контура, следовательно, магнитная проницаемость вещества не изменяются,
- вся энергия источника тока переходит в энергию магнитного поля.
Эти условия справедливы точно, только для вакуума. При помещении контура с током в вещество, следует учитывать:
- Намагничивание вещества, что ведет к увеличению ее температуры.
- Объем и плотность вещества в магнитном поле способны меняться даже при неизменной температуре.
Данные нюансы указывают на то, что магнитная проницаемость вещества ($mu$), которая изменяется при изменении температуры и плотности среды не может быть неизменной при намагничивании.
Кроме того, работа источника ЭДС не целиком переходит в энергию магнитного поля.
Выше сказанное дает основание полагать, что в общем случае формула (2) не выражает в точности работу при намагничивании и выражение (9) не дает объемную плотность энергии магнитного поля в веществе.
Допустим, что изменение объема вещества мало. Температура среды постоянна. Внешняя работа расходуется на рост энергии магнитного поля E и на теплоотдачу Q, для поддержания постоянной температуры. Работа внешних сил, в нашем случае источника тока, которая совершается над телом при квазистатическом изотермическом процессе, будет равна приращению свободной энергии тела. Получается, что формула (9) отражает часть свободной энергии намагниченного вещества, которая связана с магнитным полем.
Если количества теплоты Q в сравнении с энергией поля E мало, тогда выполняется равенство (2).
Условие неизменности магнитной проницаемости вещества, означает, что справедлива линейная зависимость (10). Даная зависимость выполняется для вакуума. Ее можно применять для парамагнетиков и диамагнетиков. Но для ферромагнетиков связь между магнитной индукцией и напряженностью магнитного поля является сильно нелинейной даже при T=const, поэтому выражение (9) для этих веществ не применяется.
Предыдущая